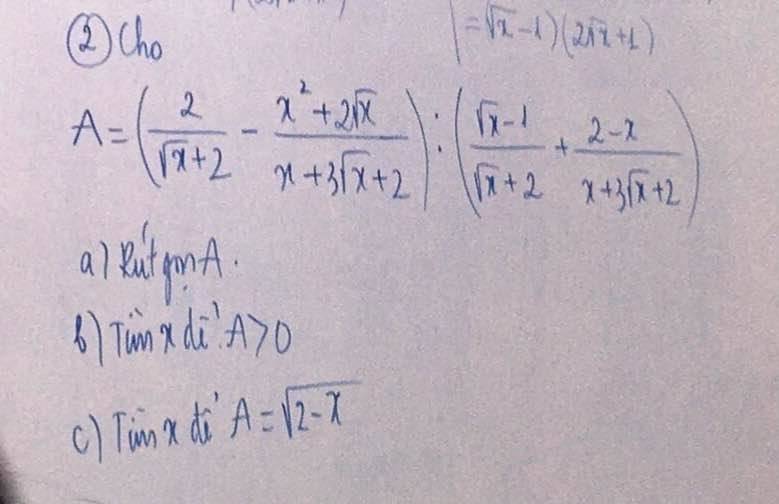đk x\(\ge0\)
\(a,A=\left(\dfrac{2}{\sqrt{x}+2}-\dfrac{x^2+2\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}\right):\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{2-x}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}\right)\\ =\left(\dfrac{2\sqrt{x}+2-x^2-2\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}\right):\left(\dfrac{x-1+2-x}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}\right)\\ =\dfrac{2-x^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}.\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}{1}\\ =2-x^2\)
b,
\(ĐểA>0\\ 2-x^2>0\\ x^2< 2\\ \left[{}\begin{matrix}x>-\sqrt{2}\\x< \sqrt{2}\end{matrix}\right.=>-\sqrt{2}< x< \sqrt{2}\)