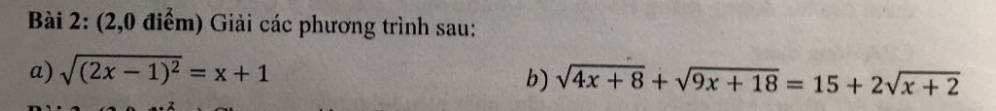`a)\sqrt{(2x-1)^2}=x+1` `ĐK: x >= -1`
`<=>|2x-1|=x+1`
`<=>[(2x-1=x+1),(2x-1=-x-1):}`
`<=>[(x=2),(x=0):}` (t/m)
Vậy `S={0;2}`
____________________________________________
`b)\sqrt{4x+8}+\sqrt{9x+18}=15+2\sqrt{x+2}` `ĐK: x >= -2`
`<=>2\sqrt{x+2}+3\sqrt{x+2}=15+2\sqrt{x+2}`
`<=>3\sqrt{x+2}=15`
`<=>\sqrt{x+2}=5`
`<=>x+2=25`
`<=>x=23` (t/m)
Vậy `S={23}`
a)
<=>4x^2-4x+1=x^2+2x+1
=>3x^2-6x=0
<=>3x(x-2)=0
\(< =>\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
b)\(\sqrt{4\left(x+2\right)}+\sqrt{9\left(x+2\right)}=15+2\sqrt{x+2}\)
<=>\(2\sqrt{x+2}+3\sqrt{x+2}=15+2\sqrt{x+2}\)
<=>\(< =>3\sqrt{x+2}=15=>9\left(x+2\right)=225\)
=>9x=207
=>x=23
`(a):`
`\sqrt{(2x-1)^{2}}=x+1`
`<=>|2x-1|=x+1\ (ĐK:x\ge -1)`
`=>2x-1=x+1` hoặc `2x-1=-(x+1)`
`<=>x=2\ (TMDK)` hoặc `x=0\ (TMDK)`
Vậy `S={2;0}`
`(b):`
`\sqrt{4x+8}+\sqrt{9x+18}=15+2\sqrt{x+2}\ (ĐK:x\ge -2)`
`<=>\sqrt{4}.\sqrt{x+2}+\sqrt{9}.\sqrt{x+2}=15+2\sqrt{x+2}`
`<=>(2+3).\sqrt{x+2}=15+2\sqrt{x+2}`
`<=>5\sqrt{x+2}=15+2\sqrt{x+2}`
`<=>3\sqrt{x+2}=15`
`<=>\sqrt{x+2}=5`
`<=>x+2=25`
`<=>x=23\ (TMDK)`
Vậy `S={23}`