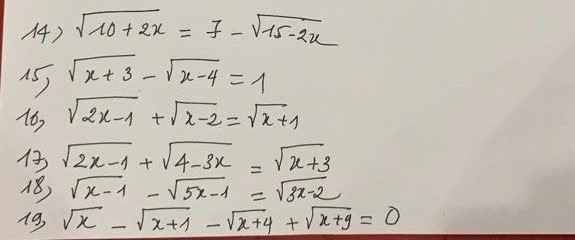14) Điều kiện: \(\left\{{}\begin{matrix}10+2x\ge0\\15-2x\ge0\end{matrix}\right.\Leftrightarrow-5\le x\le\dfrac{15}{2}\)
\(\sqrt{10+2x}=7-\sqrt{15-2x}\)
\(\Leftrightarrow\sqrt{10+2x}+\sqrt{15-2x}=7\)
\(\Leftrightarrow10+2x+15-2x+2\sqrt{\left(10+2x\right)\left(15-2x\right)}=49\)
\(\Leftrightarrow\sqrt{\left(10+2x\right)\left(15-2x\right)}=12\)
\(\Leftrightarrow\left(10+2x\right)\left(15-2x\right)=144\)
\(\Leftrightarrow150-20x+30x-4x^2=144\)
\(\Leftrightarrow6+10x-4x^2=0\)
\(\Leftrightarrow3+5x-2x^2=0\)
\(\Leftrightarrow\left(3-x\right)+\left(6x-2x^2\right)=0\)
\(\Leftrightarrow\left(3-x\right)+2x\left(3-x\right)=0\)
\(\Leftrightarrow\left(1+2x\right)\left(3-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=3\end{matrix}\right.\)
So với điều kiện thấy \(x=-\dfrac{1}{2}\) và \(x=3\) thỏa mãn.
Vậy phương trình có tập nghiệm là: \(S=\left\{-\dfrac{1}{2};3\right\}.\)
15) Điều kiện: \(\left\{{}\begin{matrix}x+3\ge0\\x-4\ge0\end{matrix}\right.\Leftrightarrow x\ge4\)
\(\sqrt{x+3}-\sqrt{x-4}=1\)
\(\Leftrightarrow\sqrt{x+3}=\sqrt{x-4}+1\)
\(\Leftrightarrow x+3=x-4+1+2\sqrt{x-4}\)
\(\Leftrightarrow\sqrt{x-4}=3\)
\(\Leftrightarrow x-4=9\)
\(\Leftrightarrow x=13\) (nhận)
Vậy phương trình có tập nghiệm là: \(S=\left\{13\right\}.\)
16) Điều kiện: \(\left\{{}\begin{matrix}2x-1\ge0\\x-2\ge0\\x+1\ge0\end{matrix}\right.\Leftrightarrow x\ge2\)
\(\sqrt{2x-1}+\sqrt{x-2}=\sqrt{x+1}\)
\(\Leftrightarrow\left(\sqrt{2x-1}-\sqrt{x+1}\right)+\sqrt{x-2}=0\)
\(\Leftrightarrow\dfrac{\left(2x-1\right)-\left(x+1\right)}{\sqrt{2x-1}+\sqrt{x+1}}+\sqrt{x-2}=0\)
\(\Leftrightarrow\dfrac{x-2}{\sqrt{2x-1}+\sqrt{x+1}}+\sqrt{x-2}=0\)
\(\Leftrightarrow\sqrt{x-2}\left(\dfrac{\sqrt{x-2}}{\sqrt{2x-1}+\sqrt{x+1}}+1\right)=0\)
\(\Leftrightarrow\sqrt{x-2}=0\) (vì \(\dfrac{\sqrt{x-2}}{\sqrt{2x-1}+\sqrt{x+1}}+1>0\))
\(\Leftrightarrow x-2=0\)
\(\Leftrightarrow x=2\) (nhận)
Vậy phương trình có tập nghiệm là: \(S=\left\{2\right\}.\)
17) Điều kiện: \(\left\{{}\begin{matrix}2x-1\ge0\\4-3x\ge0\\x+3\ge0\end{matrix}\right.\Leftrightarrow\dfrac{1}{2}\le x\le\dfrac{4}{3}\)
\(\sqrt{2x-1}+\sqrt{4-3x}=\sqrt{x+3}\)
\(\Leftrightarrow2x-1+4-3x+2\sqrt{\left(2x-1\right)\left(4-3x\right)}=x+3\)
\(\Leftrightarrow\sqrt{\left(2x-1\right)\left(4-3x\right)}=x\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(2x-1\right)\left(4-3x\right)=x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\8x-6x^2-4+3x=x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\11x-7x^2-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(11x-11x^2\right)-\left(4-4x^2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\11x\left(1-x\right)-4\left(1-x^2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\11x\left(1-x\right)-4\left(1-x\right)\left(1+x\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(1-x\right)\left[11x-4\left(1+x\right)\right]=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(1-x\right)\left(7x-4\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{4}{7}\end{matrix}\right.\)
So với điều kiện ban đầu thấy \(x=1\) và \(x=\dfrac{4}{7}\) thỏa mãn.
Vậy phương trình có tập nghiệm là: \(S=\left\{1;\dfrac{4}{7}\right\}.\)
18) Điều kiện: \(\left\{{}\begin{matrix}x-1\ge0\\5x-1\ge0\\3x-2\ge0\end{matrix}\right.\Leftrightarrow x\ge1\)
\(\sqrt{x-1}-\sqrt{5x-1}=\sqrt{3x-2}\)
\(\Leftrightarrow\sqrt{x-1}=\sqrt{5x-1}+\sqrt{3x-2}\)
\(\Leftrightarrow x-1=5x-1+3x-2+2\sqrt{\left(5x-1\right)\left(3x-2\right)}\)
\(\Leftrightarrow2-7x=2\sqrt{\left(5x-1\right)\left(3x-2\right)}\)
\(\Leftrightarrow\left\{{}\begin{matrix}2-7x\ge0\\49x^2-28x+4=4\left(5x-1\right)\left(3x-2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{2}{7}\\49x^2-28x+4=4\left(15x^2-13x+2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{2}{7}\\49x^2-28x+4=60x^2-42x+8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{2}{7}\\11x^2-14x+4=0\end{matrix}\right.\) \(\left(1\right)\)
Ta có: \(\Delta'=49-44=5>0\Rightarrow\) phương trình có hai nghiệm phân biệt là: \(\left[{}\begin{matrix}x=\dfrac{7-\sqrt{5}}{11}\\x=\dfrac{7+\sqrt{5}}{11}\end{matrix}\right.\)
Khi đó, \(\left(1\right)\Leftrightarrow\) Phương trình vô nghiệm.
Vậy phương trình vô nghiệm.