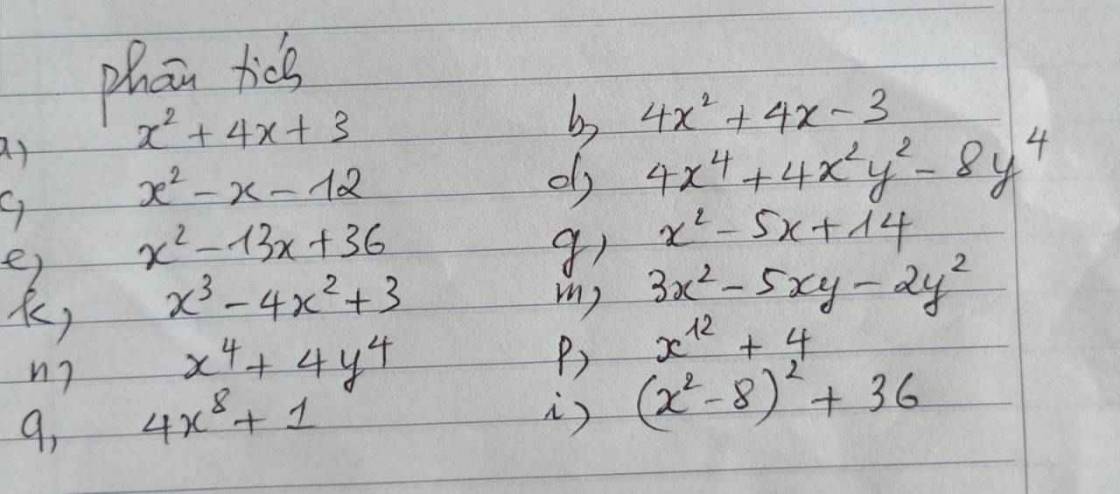\(a,=x^2+x+3x+3\\ =x\left(x+1\right)+3\left(x+1\right)\\ =\left(x+3\right)\left(x+1\right)\\ b,=4x^2+4x+1-4\\ =\left(2x+1\right)^2-4\\ =\left(2x+1-2\right)\left(2x+1+2\right)\\ =\left(2x-1\right)\left(2x+3\right)\\ c,=x^2-4x+3x-12\\ =x\left(x-4\right)+3\left(x-4\right)\\ =\left(x+3\right)\left(x-4\right)\\ d,=\left(4x^4+4x^2y^2+y^4\right)-9y^4\\ =\left(2x^2+y^2\right)^2-9y^4\\ =\left(2x^2+y^2-3y^2\right)\\ \left(2x^2+y^2+3y^2\right)\\ =\left(2x^2-2y^2\right)\left(2x^2+4y^2\right)\\ =2\left(x-y\right)\left(x+y\right).2\left(x^2+2y^2\right)\\ \)
\(e,=x^2-4x-9x+36\\ =x\left(x-4\right)-9\left(x-4\right)\\ =\left(x-9\right)\left(x-4\right)\)
a: =(x+1)(x+3)
b: =(2x+3)(2x-1)
c: =(x-4)*(x+3)
e: =(x-9)(x-4)
k: \(=x^3-x^2-3x^2+3=x^2\left(x-1\right)-3\left(x-1\right)\left(x+1\right)=\left(x-1\right)\left(x^2-3x-3\right)\)