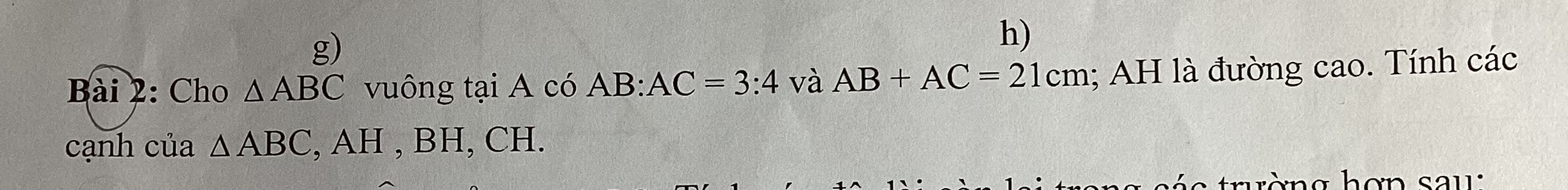Theo giả thiết, ta có: \(AB:AC=3:4\Rightarrow\dfrac{AB}{AC}=\dfrac{3}{4}\Leftrightarrow\dfrac{3}{AB}=\dfrac{4}{AC}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{3}{AB}=\dfrac{4}{AC}=\dfrac{3+4}{AB+AC}=\dfrac{7}{21}=\dfrac{1}{3}\)
\(\Rightarrow AB=3.3=9\) \(\left(cm\right)\) và \(AC=3.4=12\) \(\left(cm\right)\)
Áp dụng định lí Pytago vào tam giác ABC vuông tại A, có:
\(BC^2=AB^2+AC^2=9^2+12^2=81+144=225\Rightarrow BC=15\) \(\left(cm\right)\)
Vì tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng trong tam giác vuông, ta có:
- \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{9^2}+\dfrac{1}{12^2}=\dfrac{9^2+12^2}{9^2.12^2}=\dfrac{15^2}{108^2}\Leftrightarrow AH^2=\left(\dfrac{108}{15}\right)^2\Rightarrow AH=\dfrac{108}{15}\)\(\left(cm\right)\)
- \(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{9^2}{15}=\dfrac{27}{5}\) \(\left(cm\right)\)
- \(AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{12^2}{15}=\dfrac{48}{5}\) \(\left(cm\right)\)