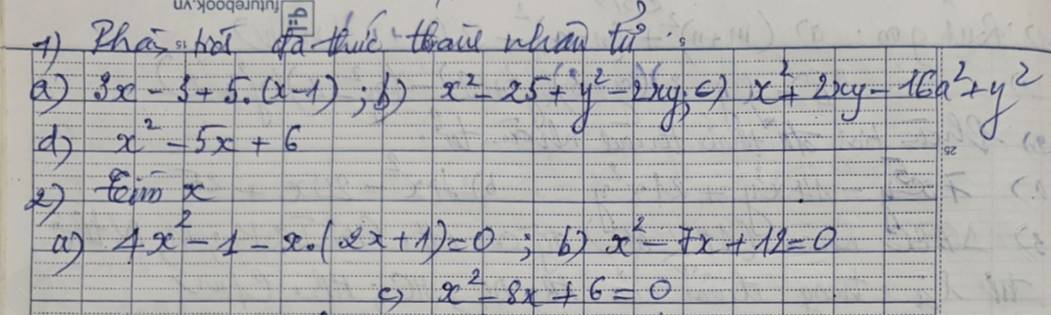Bài 2:
a: =>(2x-1)(2x+1)-x(2x+1)=0
=>(2x+1)(x-1)=0
=>x=1hoặc x=-1/2
b: =>(x-3)(x-4)=0
=>x=3 hoặc x=4
c: =>x2-8x+16-10=0
=>(x-4)2=10
hay \(x\in\left\{\sqrt{10}+4;-\sqrt{10}+4\right\}\)
`(1):`
`(a):3x-3+5(x-1)=3(x-1)+5(x-1)=(3+5)(x-1)=8(x-1)`
`(b):x^{2}-25+y^{2}-2xy=(x-y)^{2}-5^{2}=(x-y-5)(x-y+5)`
`(c):x^{2}+2xy-16a^{2}+y^{2}=(x+y)^{2}-(4a)^{2}=(x+y+4a)(x+y-4a)`
`(d):x^{2}-5x+6=(x^{2}-2x)-(3x-6)=x(x-2)-3(x-2)=(x-2)(x-3)`
`(2):`
`(a):4x^{2}-1-x(2x+1)=0<=>(2x-1)(2x+1)-x(2x+1)=0`
`<=>(2x+1)(2x-1-x)=0`
`=>2x+1=0` hoặc `x-1=0`
`<=>x=-1/2` hoặc `x=1`
`(b):x^{2}-7x+12=0<=>(x-4)(x-3)=0`
`=>x-4=0` hoặc `x-3=0`
`<=>x=4` hoặc `x=3`
`(c):x^{2}-8x+16=0<=>(x-4)^{2}=0<=>x=4`
Bài 2:
a: =>(2x-1)(2x+1)-x(2x+1)=0
=>(2x+1)(x-1)=0
=>x=1hoặc x=-1/2
b: =>(x-3)(x-4)=0
=>x=3 hoặc x=4
c: =>x2-8x+16-10=0
=>(x-4)2=10
hay x∈{√10+4;−√10+4}x∈{10+4;−10+4}
(1):(1):
(a):3x−3+5(x−1)=3(x−1)+5(x−1)=(3+5)(x−1)=8(x−1)(a):3x-3+5(x-1)=3(x-1)+5(x-1)=(3+5)(x-1)=8(x-1)
(b):x2−25+y2−2xy=(x−y)2−52=(x−y−5)(x−y+5)(b):x2-25+y2-2xy=(x-y)2-52=(x-y-5)(x-y+5)
(c):x2+2xy−16a2+y2=(x+y)2−(4a)2=(x+y+4a)(x+y−4a)(c):x2+2xy-16a2+y2=(x+y)2-(4a)2=(x+y+4a)(x+y-4a)
(d):x2−5x+6=(x2−2x)−(3x−6)=x(x−2)−3(x−2)=(x−2)(x−3)(d):x2-5x+6=(x2-2x)-(3x-6)=x(x-2)-3(x-2)=(x-2)(x-3)
(2):(2):
(a):4x2−1−x(2x+1)=0⇔(2x−1)(2x+1)−x(2x+1)=0(a):4x2-1-x(2x+1)=0⇔(2x-1)(2x+1)-x(2x+1)=0
⇔(2x+1)(2x−1−x)=0⇔(2x+1)(2x-1-x)=0
⇒2x+1=0⇒2x+1=0 hoặc x−1=0x-1=0
⇔x=−12⇔x=-12 hoặc x=1
(1):(1):
(a):3x−3+5(x−1)=3(x−1)+5(x−1)=(3+5)(x−1)=8(x−1)(a):3x-3+5(x-1)=3(x-1)+5(x-1)=(3+5)(x-1)=8(x-1)
(b):x2−25+y2−2xy=(x−y)2−52=(x−y−5)(x−y+5)(b):x2-25+y2-2xy=(x-y)2-52=(x-y-5)(x-y+5)
(c):x2+2xy−16a2+y2=(x+y)2−(4a)2=(x+y+4a)(x+y−4a)(c):x2+2xy-16a2+y2=(x+y)2-(4a)2=(x+y+4a)(x+y-4a)
(d):x2−5x+6=(x2−2x)−(3x−6)=x(x−2)−3(x−2)=(x−2)(x−3)(d):x2-5x+6=(x2-2x)-(3x-6)=x(x-2)-3(x-2)=(x-2)(x-3)
(2):(2):
(a):4x2−1−x(2x+1)=0⇔(2x−1)(2x+1)−x(2x+1)=0(a):4x2-1-x(2x+1)=0⇔(2x-1)(2x+1)-x(2x+1)=0
⇔(2x+1)(2x−1−x)=0⇔(2x+1)(2x-1-x)=0
⇒2x+1=0⇒2x+1=0 hoặc x−1=0x-1=0
⇔x=−12⇔x=-12 hoặc x=1x=1
(b):x2−7x+12=0⇔(x−4)(x−3)=0(b):x2-7x+12=0⇔(x-4)(x-3)=0
⇒x−4=0⇒x-4=0 hoặc x−3=0x-3=0
⇔x=4⇔x=4 hoặc x=3x=3
(c):x2−8x+16=0⇔(x−4)2=0⇔x=4