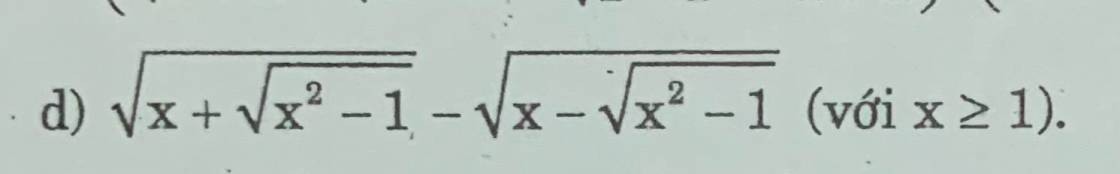Question

Answer 1

Với x > = 1 

\(A=\sqrt{x+\sqrt{x^2-1}}-\sqrt{x-\sqrt{x^2-1}}\)

\(A^2=x+\sqrt{x^2-1}-2\sqrt{x^2-\left(x^2-1\right)}+x-\sqrt{x^2-1}=2x-2\Rightarrow A=\sqrt{2}\sqrt{x-1}\)

Answer 2

\(=\left(\sqrt{x+\sqrt{x^2-1}}\right)^2-\left(\sqrt{x-\sqrt{x^2-1}}\right)^2\\ =x+\sqrt{x^2-1}-x+\sqrt{x^2-1}\\ =2\sqrt{x^2-1}\\ =2\sqrt{\left(x-1\right)\left(x+1\right)}\)