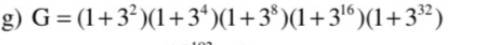\(\left(3^2-1\right)G=\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(1+3^{16}\right)\left(1+3^{32}\right)=\left(3^8-1\right)\left(3^8+1\right)\left(1+3^{16}\right)\left(1+3^{32}\right)\)
\(=\left(3^{16}-1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)=\left(3^{32}-1\right)\left(3^{32}+1\right)=3^{64}-1\Rightarrow G=\dfrac{3^{64}-1}{8}\)
\(\Rightarrow\left(1-3^2\right)G=\left(1-3^2\right)\left(1+3^2\right)\left(1+3^4\right)\left(1+3^8\right)\left(1+3^{16}\right)\left(1+3^{32}\right)\)
\(=\left(1-3^4\right)\left(1+3^4\right)\left(1+3^8\right)\left(1+3^{16}\right)\left(1+3^{32}\right)\)
\(=\left(1-3^8\right)\left(1+3^8\right)\left(1+3^{16}\right)\left(1+3^{32}\right)\)
\(=\left(1-3^{16}\right)\left(1+3^{16}\right)\left(1+3^{32}\right)\)
\(=\left(1-3^{32}\right)\left(1+3^{32}\right)=1-3^{64}\)
\(\Rightarrow G=\dfrac{1-3^{64}}{1-3^2}=\dfrac{3^{64}-1}{8}\)