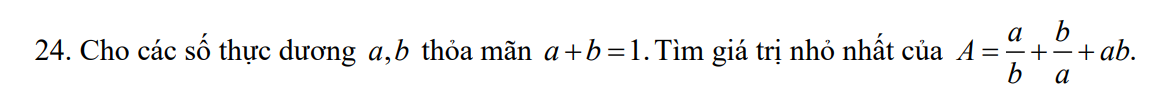\(a+b\ge2\sqrt{ab}\) \((BĐT\ Cô\ Si)\)
\(< =>1\ge2\sqrt{ab}\\ < =>\sqrt{ab}\le\dfrac{1}{2}\\ < =>0< ab\le\dfrac{1}{4}\)
\(A=\dfrac{a}{b}+\dfrac{b}{a}+ab\)
\(=\left(\dfrac{a}{b}+4ab\right)+\left(\dfrac{b}{a}+4ab\right)-7ab\ge2\sqrt{\dfrac{a}{b}.4ab}+2\sqrt{\dfrac{b}{a}.4ab}-7ab\) \((BĐT\ Cô\ Si)\)
\(=>A\ge2\sqrt{4a^2}+2\sqrt{4b^2}-7ab\ge2.2a+2.2b-7.\dfrac{1}{4}=4\left(a+b\right)-\dfrac{7}{4}=4.1-\dfrac{7}{4}=\dfrac{9}{4}\)
\(Dấu''=''\ xảy\ ra\ khi:\) \(\left\{{}\begin{matrix}a=b>0\\\dfrac{a}{b}=4ab\\\dfrac{b}{a}=4ab\\a+b=1\end{matrix}\right.< =>a=b=\dfrac{1}{2}\)
\(Vậy\ GTNN\ của\ A\ là :\) \(\dfrac{9}{4}< =>a=b=\dfrac{1}{2}\)