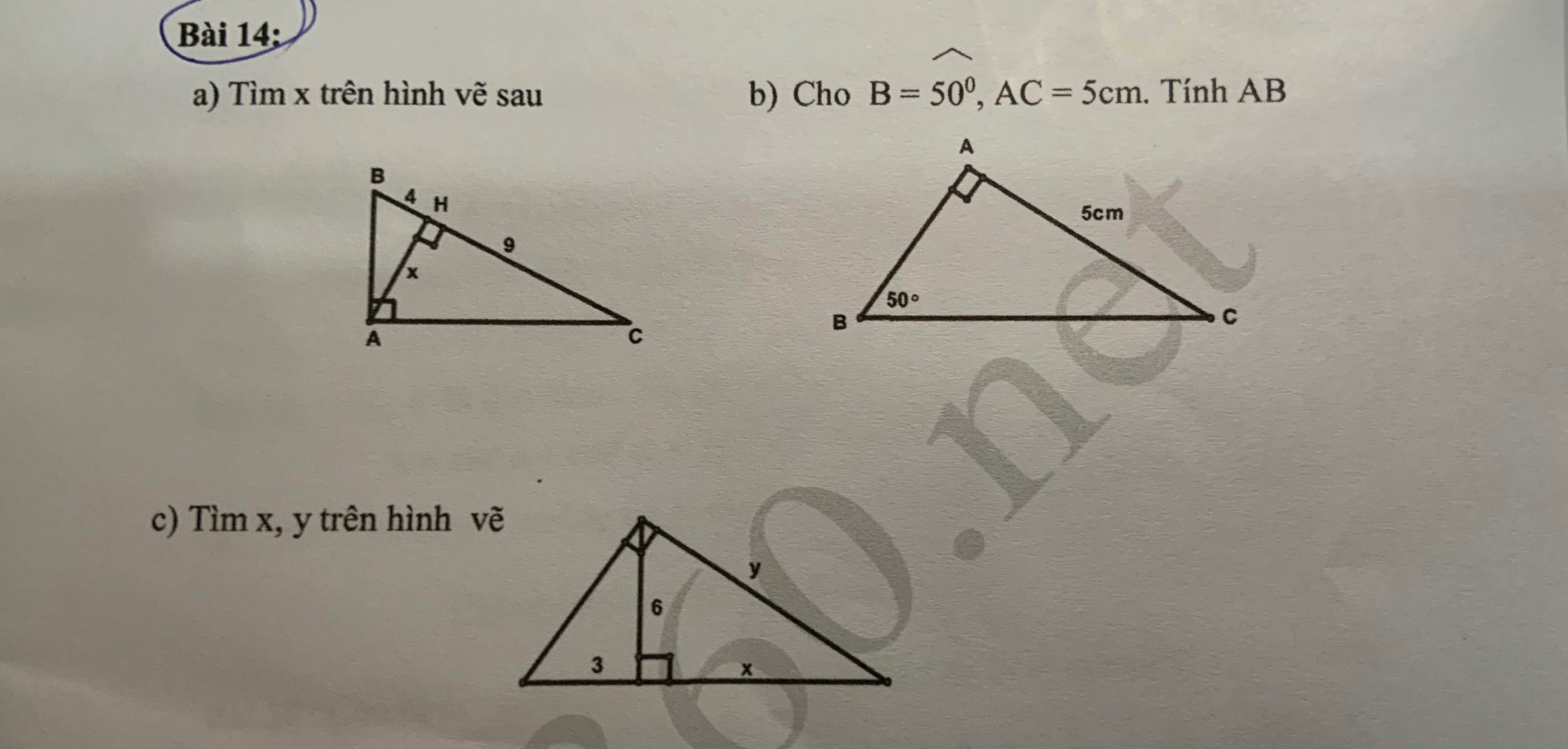
a. \(AH^2=HC+BH\\ \Rightarrow AH^2=4+9\\ \Rightarrow AH^2=13\\ \Rightarrow AH^{ }=\sqrt{13}\)
b. \(\tan B=\dfrac{AC}{AB}\\ \Rightarrow AB=\dfrac{AC}{\tan B}\\ \Rightarrow AB=\dfrac{5}{\tan50^o}\\ \Rightarrow AB\approx4,19\left(cm\right)\)
a) \(\Delta ABC\) vuông tại A có: AH là đường cao.
\(\Rightarrow AH^2=BH.CH\) (hệ thức lượng trong tam giác vuông).
\(\Rightarrow x=\sqrt{BH.CH}=\sqrt{4.9}=6\left(cm\right)\)
b) \(\Delta ABC\) vuông tại A có:
\(\tan\widehat{B}=\dfrac{AC}{AB}\)
\(\Rightarrow\dfrac{5}{AB}=\tan50^0\)
\(\Rightarrow AB=\dfrac{5}{\tan50^0}\approx4,20^0\)