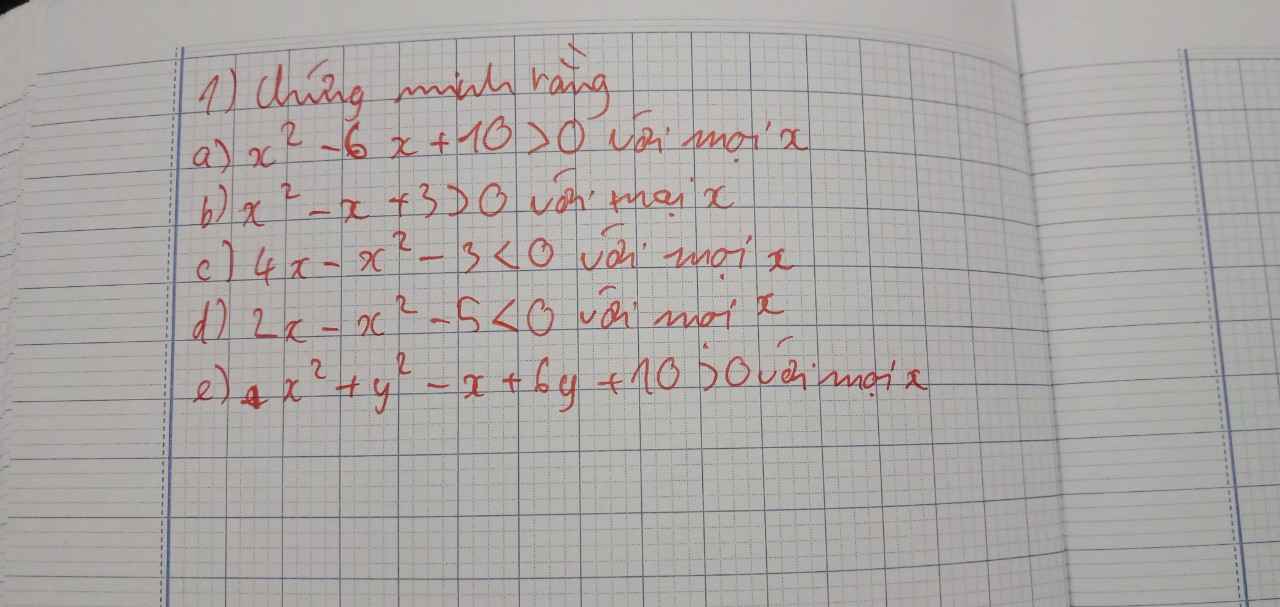`a, x^2 - 6x + 10 = x^2 - 6x + 9 + 1 = (x-3)^2 + 1 >= 0 + 1 = 1 >0`.
`b, x^2 -x + 3 = x^2 - x + 1/4 + 11/4 = (x-1/2)^2 + 11/4 >= 0+11/4 = 11/4 > 0`
`c, 4x -x^2 - 3 < 0 = -(x^2 + 4x + 4) - 1 = -(x-2)^2 - 1 < 0 - 1 = -1 < 0`
`d, - x^2 + 2x - 5 = -(x^2 - 2x + 5) = -(x-1)^2 - 4 <= 0 - 4 = -4 < 0`.
`e, x^2 + y^2 - x + 6y + 10 = y^2 + 6y + 9 + x^2 - x + 1/4 + 3/4`
`= (y+3)^2 + (x-1/2)^2 + 3/4 >= 0 + 0 + 3/4 = 3/4 > 0 forall x in RR`
a: \(=x^2-6x+9+1=\left(x-3\right)^2+1>0\forall x\)
b: \(=x^2-x+\dfrac{1}{4}+\dfrac{11}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall x\)
c: \(=-\left(x^2-4x+3\right)\)
\(=-\left(x^2-4x+4-1\right)\)
\(=-\left(x-2\right)^2+1< =1\forall x\)
d: \(=-\left(x^2-2x+5\right)\)
\(=-\left(x^2-2x+1+4\right)\)
\(=-\left(x-1\right)^2-4< 0\forall x\)