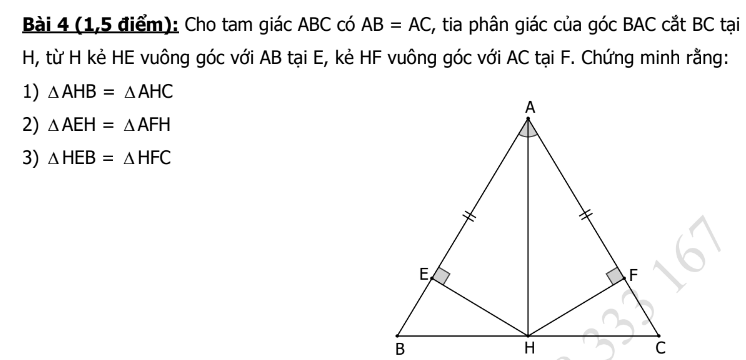
1: Xét ΔAHB và ΔAHC có
AH chung
góc BAH=góc CAH
AB=AC
DO đó: ΔAHB=ΔAHC
2: Xét ΔAEH vuông tạiE và ΔAFH vuông tại F có
AH chung
góc EAH=góc FAH
Do đó: ΔAEH=ΔAFH
3: Xét ΔHEB vuông tại E và ΔHFC vuông tại F có
HB=HC
góc B=góc C
Do đó: ΔHEB=ΔHFC
`1)`Xét tam giác vuông AHB và tam giác vuông AHC, có:
\(AB=AC\) ( gt )
\(\widehat{B}=\widehat{C}\) ( gt )
Vậy tam giác vuông AHB`=` tam giác vuông AHC ( ch.gn )
`2)`Xét tam giác vuông AEH và tam giác vuông AFH, có:
`AH`: chung
\(\widehat{EAH}=\widehat{FAH}\)
Vậy tam giác vuông AEH `=` tam giác vuông AFH ( ch.gn )
`3)`Xét tam giác vuông HEB và tam giác vuông HFC, có:
`HB=HC` ( ABC cân; AH là đường phân giác )
\(\widehat{B}=\widehat{C}\) ( gt )
Vậy tam giác vuông HEB `=` tam giác vuông HFC ( ch.gn )
a, Xét tam giác AHB và AHC ta có
AB = AC
góc BAH = góc CAH
HB = HC
=> tam giác AHB = AHC (cgc)
b, Xét tam giác EAH và FAH có
góc E = góc H = 90 độ
AH chung
góc BAH = góc CAH
=> tam giác AEH = FAH (ch,gn)
=> EH = HF ( 2 cạnh t,ứng )
ý c, Xét tam giác HEB và tam giác HFC có
EH = HF
góc E = góc F = 90 độ
BH = HC
=> tam giác ... = tam giác ...