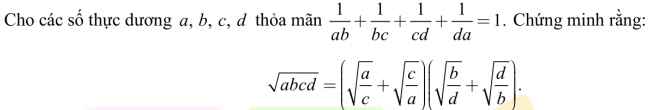\(a,b,c,d>0\).
\(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{cd}+\dfrac{1}{da}=1\)
\(\Rightarrow\dfrac{cd+da+ab+bc}{abcd}=1\)
\(\Rightarrow ab+bc+cd+da=abcd\)
\(\Rightarrow b\left(a+c\right)+d\left(a+c\right)=abcd\)
\(\Rightarrow\left(a+c\right)\left(b+d\right)=abcd\)
\(\left(\sqrt{\dfrac{a}{c}}+\sqrt{\dfrac{c}{a}}\right)\left(\sqrt{\dfrac{b}{d}}+\sqrt{\dfrac{d}{b}}\right)=\dfrac{a+c}{\sqrt{ca}}.\dfrac{b+d}{\sqrt{db}}=\dfrac{\left(a+c\right)\left(b+d\right)}{\sqrt{abcd}}=\dfrac{abcd}{\sqrt{abcd}}=\sqrt{abcd}\left(đpcm\right)\)
Đúng 2
Bình luận (0)
