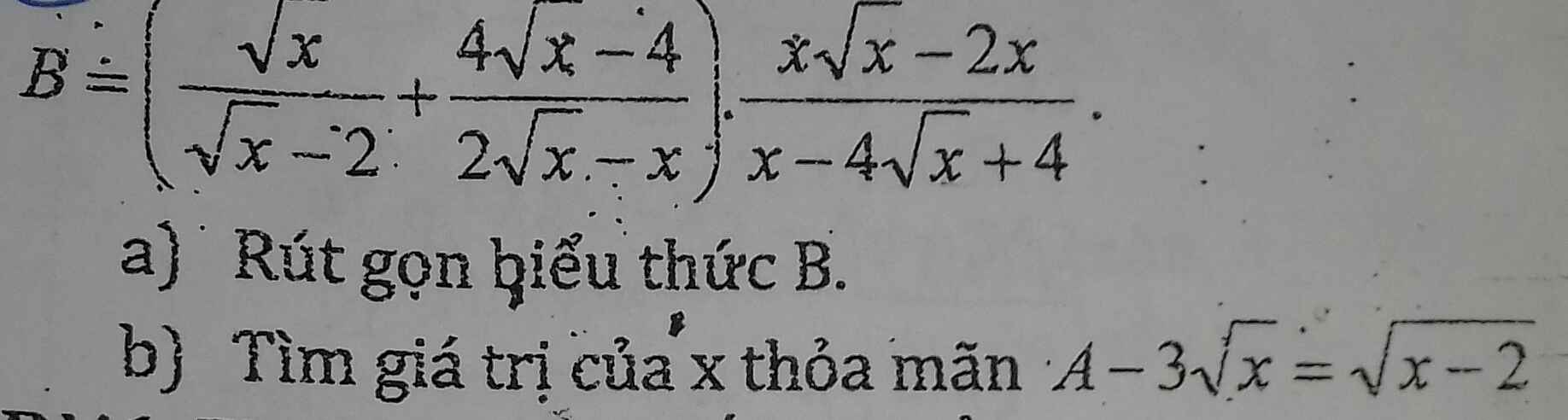a/ \(B=\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}+\dfrac{4\sqrt{x}-4}{\sqrt{x}\left(2-\sqrt{x}\right)}\right).\dfrac{x\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)^2}=\left(\dfrac{x-4\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}\right).\dfrac{x}{\sqrt{x}-2}=\dfrac{\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)}.\sqrt{x}=\sqrt{x}\)
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne4\end{matrix}\right.\)
\(\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}+\dfrac{4\sqrt{x}-4}{2\sqrt{x}-x}\right).\dfrac{x\sqrt{x}-2x}{x-4\sqrt{x}+4}\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-2\right)}\right).\dfrac{x\left(\sqrt{x}-2\right)}{x-4\sqrt{x}+4}\)
\(=\dfrac{x-4\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}.\dfrac{x\left(\sqrt{x}-2\right)}{x-4\sqrt{x}+4}\)
\(=\dfrac{x}{\sqrt{x}}\)
\(=\sqrt{x}\)