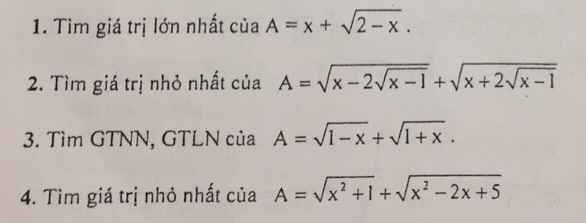\(1\left(đk:x\le2\right).A=x+\sqrt{2-x}\)
\(\Leftrightarrow A-x=\sqrt{2-x}\Leftrightarrow A^2-2Ax+x^2=2-x\)
\(\Leftrightarrow x^2-x\left(2A-1\right)+A^2-2=0\)
\(\Rightarrow\Delta\ge0\Leftrightarrow\left(2A-1\right)^2-4\left(A^2-2\right)\ge0\Leftrightarrow A\le\dfrac{9}{4}\)
\(dấu"="\Leftrightarrow x=\dfrac{7}{4}\)
\(3\left(đk:-1\le x\le1\right).A=\sqrt{1-x}+\sqrt{1+x}\le\sqrt{2\left(1-x+1+x\right)}=2\)
\(A^2=2+2\sqrt{\left(1-x\right)\left(1+x\right)}\ge2\Rightarrow A\ge\sqrt{2}\)
\(\Rightarrow max=2\Leftrightarrow x=0;min=\sqrt{2}\Leftrightarrow x=-1\)
\(2.A=\sqrt{x-2\sqrt{x-1}}+\sqrt{x+2\sqrt{x-1}}=\sqrt{\left(x-1\right)-2\sqrt{x-1}+1}+\sqrt{\left(x-1\right)+2\sqrt{x-1}+1}=\sqrt{\left(\sqrt{x-1}-1\right)^2}+\sqrt{\left(\sqrt{x-1}+1\right)^2}=\left|\sqrt{x-1}-1\right|+\left|\sqrt{x-1}+1\right|=\left|1-\sqrt{x-1}\right|+\left|\sqrt{x-1}+1\right|\ge\left|2\right|=2\)
\(4.A=\sqrt{x^2+1}+\sqrt{\left(x-1\right)^2+4}=\sqrt{x^2+1}+\sqrt{\left(1-x\right)^2+2^2}\ge\sqrt{\left(x+1-x\right)^2+\left(1+2\right)^2}=\sqrt{10}\left(minicopxki\right)\)
\(dấu"="\Leftrightarrow\dfrac{x}{1}=\dfrac{1-x}{2}\Leftrightarrow x=\dfrac{1}{3}\)