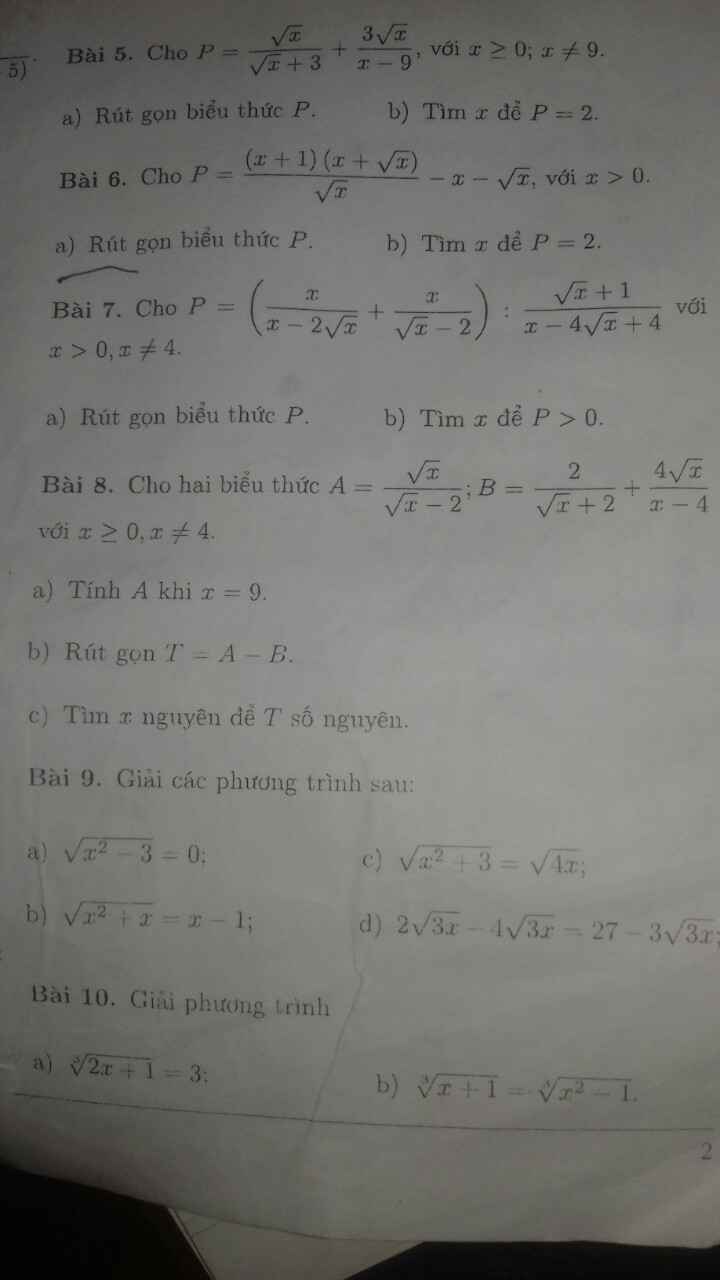Bài 9
a)\(\sqrt{x^2-3}=0\)
`<=> x^2 -3 =0`
`<=> x^2 = 3`
\(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{3}\\x=-\sqrt{3}\end{matrix}\right.\)
Vậy `S={\sqrt{3};-\sqrt{3} }`
b)\(\sqrt{x^2+x}=x-1\)
`<=>x^2 +x = x^2 -2x+1`
`<=> x^2 +x -x^2 +2x-1=0`
`<=>3x-1=0`
`<=> x =1/3`
Vậy `S={1/3}`
e lm đc thế thôi , thông cảm
c)\(\sqrt{x^2+3}=\sqrt{4x}\)
`<=> x^2 + 3 = 4x`
`<=> x^2 -4x +3 =0`
ta có : `\Delta = (-4)^2 - 4.3 = 4 >0`
=> Pt có 2 nghiệm phân biệt
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2.a}=\dfrac{-\left(-4\right)+\sqrt{4}}{2.1}\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(-4\right)-\sqrt{4}}{2.1}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{4+2}{2}=3\\x^2=\dfrac{4-2}{2}=1\end{matrix}\right.\)
Bài 10
a)`\root{3}{2x+1} = 3`
`<=> 2x+1 =27`
`<=> 2x=26`
`<=> x =13`
Vậy `S={13}`
b)`\root{3}{x+1}=\root{3}{x^2 -1}`
`<=> x +1 = x^2 -1`
`<=> x + 1 - x^2 +1=0`
`<=> x -x^2 +2 =0`
`<=> x + x^2 -2=0`
`<=> x + x^2 - 2x-2=0`
`<=> (x-2)(x+1) =0`
`<=>`\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Vậy `S={2;-1}`
e lm đc thế thôi , thông cảm
c)\(\sqrt{x^2+3}=\sqrt{4x}\)
`<=> x^2 + 3 = 4x`
`<=> x^2 -4x +3 =0`
ta có : `\Delta = (-4)^2 - 4.3 = 4 >0`
=> Pt có 2 nghiệm phân biệt
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2.a}=\dfrac{-\left(-4\right)+\sqrt{4}}{2.1}\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(-4\right)-\sqrt{4}}{2.1}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{4+2}{2}=3\\x^2=\dfrac{4-2}{2}=1\end{matrix}\right.\)
Bài 10
a)`\root{3}{2x+1} = 3`
`<=> 2x+1 =27`
`<=> 2x=28`
`<=> x =14`
Vậy `S={14}`
b)`\root{3}{x+1}=\root{3}{x^2 -1}`
`<=> x +1 = x^2 -1`
`<=> x + 1 - x^2 +1=0`
`<=> x -x^2 +2 =0`
`<=> x + x^2 -2=0`
`<=> x + x^2 - 2x-2=0`
`<=> (x-2)(x+1) =0`
`<=>`\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Vậy `S={2;-1}`