\(a)\)
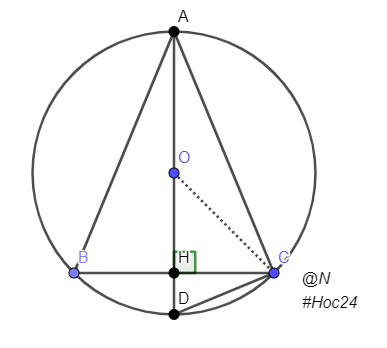
\(ΔABC\) cân tại `A`nên `AH` là đg trung trực của `BC`.
Do đó `AD` là đường trung trực của `BC`
Vì `O` nằm trên đg trung trực của `BC` nên `O` nằm trên `AD`
Vậy `AD` là đường kính của đg tròn `(O)`
\(b,\)
\(\Delta ACD\) nối tiếp đường tròn đường kính `AD` nên `hat(ACD)=90^o`
\(c,\)
Ta có :\(BH=HC=\dfrac{BC}{2}=12\left(cm\right)\)
\(\Delta AHC\) vuông tại \(H\) nên
\(AH^2=AC^2-HC^2=20^2-12^2=256\\ \Rightarrow AH=16\left(cm\right)\\ AC^2=AD\cdot AH\\ AD=\dfrac{AC^2}{AH}=25\left(cm\right)\)
Bán kính của đường tròn `(O)=12,5cm`
Đúng 4
Bình luận (0)
