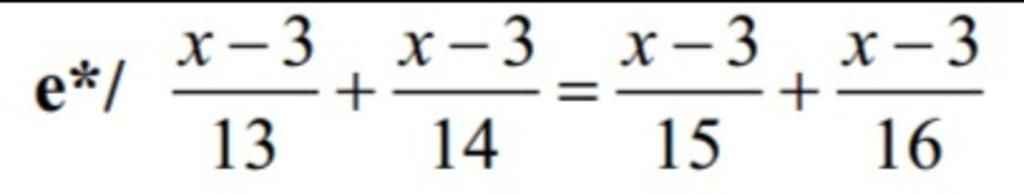\(\Leftrightarrow\left(x-3\right)\left(\dfrac{1}{13}+\dfrac{1}{14}-\dfrac{1}{15}-\dfrac{1}{16}\right)=0\)
=>x-3=0
hay x=3
`#ava`
`e)`\(\dfrac{x-3}{13}+\dfrac{x-3}{14}=\dfrac{x-3}{15}+\dfrac{x-3}{16}\)
\(\dfrac{x-3}{13}+\dfrac{x-3}{14}-\dfrac{x-3}{15}-\dfrac{x-3}{16}=0\)
\(\left(x-3\right)\left(\dfrac{1}{13}+\dfrac{1}{14}-\dfrac{1}{15}-\dfrac{1}{16}\right)=0\)
Mà : \(\dfrac{1}{13}+\dfrac{1}{14}-\dfrac{1}{15}-\dfrac{1}{16}\ne0\)
\(⇒ x − 3 = 0\)
`x=3`
Vậy `x=3`
\(\Leftrightarrow\left(x-3\right).\left(\dfrac{1}{13}+\dfrac{1}{14}\right)=\left(x-3\right)\left(\dfrac{1}{15}+\dfrac{1}{16}\right)\)
\(\Leftrightarrow\left(x-3\right)\left(\dfrac{1}{13}+\dfrac{1}{14}-\dfrac{1}{15}-\dfrac{1}{16}\right)=0\)
\(\Leftrightarrow\left(x-3\right)=0\Rightarrow x=3\)
<=>x-3/13 + x-3/14 -x-3/15 -x-3/16=0
<=>(x-3) .( 1/13+1/14-1/15-1/16)
<=>(x-3) =0 vi ( 1/13 + 1/14 -1/15-1/16 >0)
<=>x-3 =0 => x-3
vay x-3