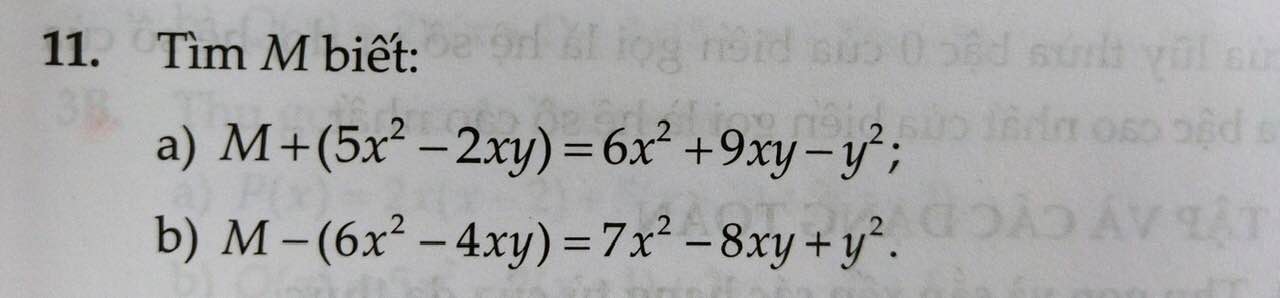a) Ta có: \(M+\left(5x^2-2xy\right)=6x^2+9xy-y^2\)
\(\Leftrightarrow M=6x^2+9xy-y^2-5x^2+2xy\)
hay \(M=x^2+11xy-y^2\)
Vậy: \(M=x^2+11xy-y^2\)
Đúng 0
Bình luận (0)
b) Ta có: \(M-\left(6x^2-4xy\right)=7x^2-8xy+y^2\)
\(\Leftrightarrow M=7x^2-8xy+y^2+6x^2+4xy\)
hay \(M=13x^2-4xy+y^2\)
Vậy: \(M=13x^2-4xy+y^2\)
Đúng 0
Bình luận (0)
a) Ta có: M+(5x2−2xy)=6x2+9xy−y2M+(5x2−2xy)=6x2+9xy−y2
⇔M=6x2+9xy−y2−5x2+2xy⇔M=6x2+9xy−y2−5x2+2xy
hay M=x2+11xy−y2M=x2+11xy−y2
Vậy: M=x2+11xy−y2
Đúng 0
Bình luận (0)
