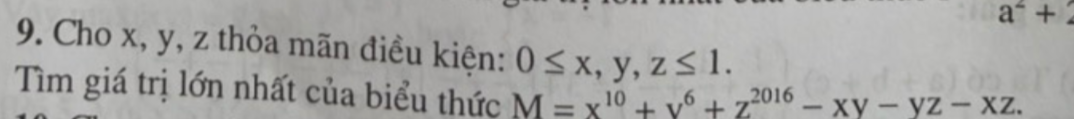Do \(0\le x;y;z\le1\Rightarrow\left\{{}\begin{matrix}x^{10}\le x\\y^6\le y\\z^{2016}\le z\end{matrix}\right.\)
\(\Rightarrow M\le x+y+z-xy-yz-zx\)
Cũng do \(0\le x;y;z\le1\Rightarrow\left(1-x\right)\left(1-y\right)\left(1-z\right)\ge0\)
\(\Rightarrow M\le1-xyz-\left(1-x-y-z+xy+yz+zx-xyz\right)\)
\(\Rightarrow M\le1-xyz-\left(1-x\right)\left(1-y\right)\left(1-z\right)\le1-xyz\le1\)
\(M_{max}=1\) khi \(\left(x;y;z\right)=\left(0;0;1\right)\); \(\left(1;1;0\right)\) và các hoán vị
Do \(0\le x;y;z\le1\Rightarrow\left\{{}\begin{matrix}x^{10}\le x\\y^6\le y\\z^{2016}\le z\end{matrix}\right.\)
\(\Rightarrow M\le x+y+z-xy-yz-zx\)
Cũng do \(0\le x;y;z\le1\Rightarrow\left(1-x\right)\left(1-y\right)\left(1-z\right)\ge0\)
\(\Rightarrow M\le1+xyz-\left(1-x-y-z+xy+yz+zx-xyz\right)\)
\(\Rightarrow M\le1+xyz-\left(1-x\right)\left(1-y\right)\left(1-z\right)\le1+xyz\le1\)
\(M_{max}=1\) khi \(\left(x;y;z\right)=\left(0;0;1\right)\); \(\left(1;1;0\right)\) và các hoán vị