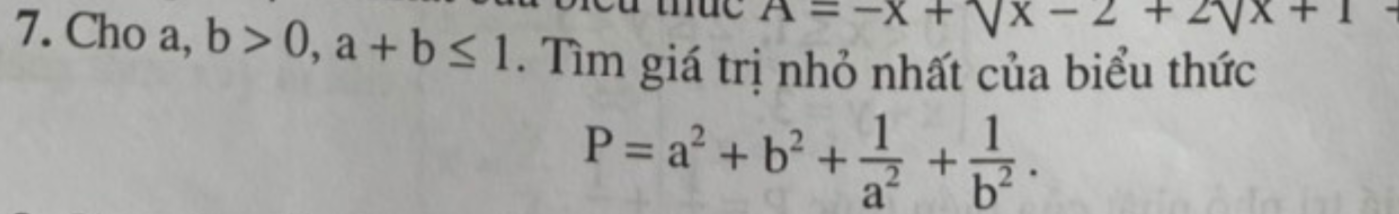Ta có:
\(P=\left(a^2+\dfrac{1}{16a^2}\right)+\left(b^2+\dfrac{1}{16b^2}\right)+\dfrac{15}{16}\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}\right)\)
Theo bddt AM - GM , ta có:
\(a^2+16a^2\ge\dfrac{1}{2};b^2+16b^2\ge\dfrac{1}{2};\)
\(\dfrac{1}{a^2}+\dfrac{1}{b^2}=\dfrac{1}{2}\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}\right)+\dfrac{1}{2}\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}\right)\ge\dfrac{2}{a^2+b^2}+\dfrac{2}{ab}\ge\dfrac{8}{\left(a+b\right)^2}=8\)
Từ đó :\(P_{min}=\dfrac{17}{2}\Leftrightarrow a=h=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
