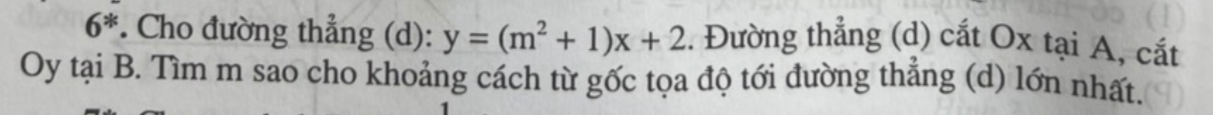(d) cắt Ox tại A => Tọa độ A(0 ; y1)
=> y1 = (m2 + 1).0 + 2 = 2 => A(0 ; 2)
(d) cắt Oy tại B => Tọa độ B(x1 ; 0)
=> 0 = (m2 + 1)x1 + 2
=> x1 = \(\dfrac{-2}{m^2+1}\)
=> B(\(\dfrac{-2}{m^2+1};0\))
Gọi khoảng cách O đến (d) : OH
=> \(\dfrac{1}{OH^2}=\dfrac{1}{ \left|\dfrac{-2}{m^2+1}\right|^2}+\dfrac{1}{2^2}\)
\(=\dfrac{\left(m^2+1\right)^2+1}{4}\)
OH max <=> OH2 max <=> \(\dfrac{1}{OH^2}min\Leftrightarrow\dfrac{\left(m^2+1\right)^2+1}{4}min\)
Khi đó \(\dfrac{\left(m^2+1\right)^2+1}{4}=\dfrac{m^4+2m^2+2}{4}\ge\dfrac{2}{4}=\dfrac{1}{2}\)
=> \(\dfrac{1}{OH^2}\ge\dfrac{1}{2}\Leftrightarrow OH\le\sqrt{2}\) ("=" khi m = 0)
Vậy m = 0 thì OHmax = \(\sqrt{2}\)