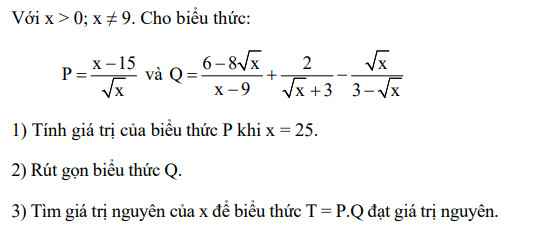\(1,\)Thay \(x=25\) vào \(P\) , ta được :
\(P=\dfrac{25-15}{\sqrt{25}}=\dfrac{10}{5}=2\)
\(\)Vậy \(P=2\) khi \(x=25\)
\(2,Q=\dfrac{6-8\sqrt{x}}{x-9}+\dfrac{2}{\sqrt{x}+3}-\dfrac{\sqrt{x}}{3-\sqrt{x}}\)
\(=\dfrac{6-8\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{2}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}\)
\(=\dfrac{6-8\sqrt{x}+2\left(\sqrt{x}-3\right)+\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{6-8\sqrt{x}+2\sqrt{x}-6+x+3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{-3\sqrt{x}+x}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
Vậy \(Q=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)