Bài 4:
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b:
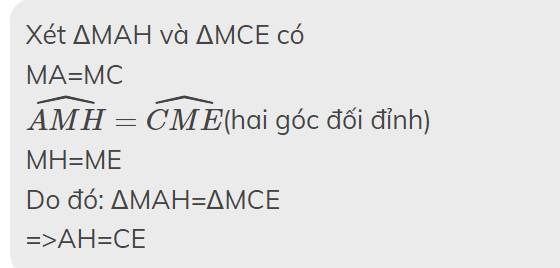
c:
Ta có;ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét ΔABC có
H,M lần lượt là trung điểm của CB,CA
=>HM là đường trung bình của ΔABC
=>HM//AB
d: Ta có: HM//AB
E\(\in\)HM
Do đó: HE//AB
Xét ΔMAE và ΔMCH có
MA=MC
\(\widehat{AME}=\widehat{CMH}\)(hai góc đối đỉnh)
ME=MH
Do đó; ΔMAE=ΔMCH
=>\(\widehat{MAE}=\widehat{MCH}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//CH
=>AE//BH
Xét tứ giác AEHB có
AE//HB
AB//HE
Do đó: AEHB là hình bình hành
=>AH cắt EB tại trung điểm của mỗi đường
mà O là trung điểm của AH
nên O là trung điểm của BE
=>B,O,E thẳng hàng
bài 3:
a: ΔMEP vuông tại E
=>\(EP^2+EM^2=MP^2\)
=>\(EP^2=10^2-6^2=64\)
=>\(EP=\sqrt{64}=8\left(cm\right)\)
b: Xét ΔMEP có EM<EP<PM
mà \(\widehat{P};\widehat{N};\widehat{E}\) lần lượt là góc đối diện của các cạnh EM,EP,PM
nên \(\widehat{P}< \widehat{N}< \widehat{E}\)














