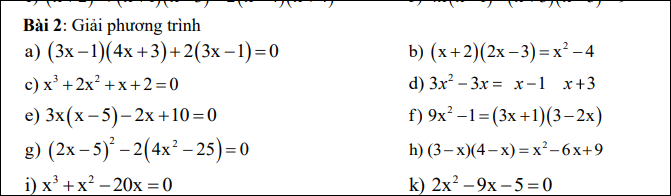\(a.\left(3x-1\right)\left(4x+3\right)+2\left(3x-1\right)=0.\\ \Leftrightarrow\left(3x-1\right)\left(4x+5\right)=0.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}.\\x=\dfrac{-5}{4}.\end{matrix}\right.\)
\(b.\left(x+2\right)\left(2x-3\right)=x^2-4.\\ \Leftrightarrow\left(x+2\right)\left(2x-3\right)-\left(x+2\right)\left(x-2\right)=0.\\ \Leftrightarrow\left(x+2\right)\left(2x-3-x+2\right)=0.\\ \Leftrightarrow\left(x+2\right)\left(x-1\right)=0.\\ \Leftrightarrow\left[{}\begin{matrix}x=-2.\\x=1.\end{matrix}\right.\)
\(c.x^3+2x^2+x+2=0.\\ \Leftrightarrow x^2\left(x+2\right)+\left(x+2\right)=0.\\ \Leftrightarrow\left(x^2+1\right)\left(x+2\right)=0.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+1=0.\\x+2=0.\end{matrix}\right.\) \(\Leftrightarrow x=-2.\)
\(e.3x\left(x-5\right)-2x+10=0.\\ \Leftrightarrow3x\left(x-5\right)-2\left(x-5\right)=0.\\ \Leftrightarrow\left(3x-2\right)\left(x-5\right)=0.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}.\\x=5.\end{matrix}\right.\)
\(f.9x^2-1=\left(3x+1\right)\left(3-2x\right).\\ \Leftrightarrow\left(3x+1\right)\left(3x-1\right)-\left(3x+1\right)\left(3-2x\right)=0.\\ \Leftrightarrow\left(3x+1\right)\left(3x-1-3+2x\right)=0.\\ \Leftrightarrow\left(3x+1\right)\left(5x-4\right)=0.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{3}.\\x=\dfrac{4}{5}.\end{matrix}\right.\)