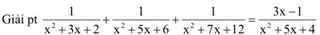Question

Answer 1

ĐKXĐ:\(x\ne-1;-2;-3;-4;-5\)

\(\dfrac{1}{x^2+3x+2}+\dfrac{1}{x^2+5x+6}+\dfrac{1}{x^2+7x+12}=\dfrac{3x-1}{x^2+5x+4}\\ \Leftrightarrow\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}=\dfrac{3x-1}{\left(x+1\right)\left(x+4\right)}\\ \Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+2}+...+\dfrac{1}{x+3}-\dfrac{1}{x+4}=\dfrac{3x-1}{\left(x+1\right)\left(x+4\right)}\\ \\ \Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+4}=\dfrac{3x-1}{\left(x+1\right)\left(x+4\right)}\)

\(\Leftrightarrow\dfrac{x+4-x-1}{\left(x+1\right)\left(x+4\right)}=\dfrac{3x-1}{\left(x+1\right)\left(x+4\right)}\\ \Leftrightarrow\dfrac{3}{\left(x+1\right)\left(x+4\right)}=\dfrac{3x-1}{\left(x+1\right)\left(x+4\right)}\\ \Leftrightarrow3x-1=3\\ \Leftrightarrow3x=4\\ \Leftrightarrow x=\dfrac{4}{3}\left(tm\right)\)

Answer 2

\(\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}=\dfrac{3x-1}{x^2+5x+4}\)

\(\Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}=\dfrac{3x-1}{x^2+5x+4}\)

\(\Leftrightarrow\dfrac{x+4-x-1}{\left(x+1\right)\left(x+4\right)}=\dfrac{3x-1}{x^2+5x+4}\Rightarrow-3=3x-1\Leftrightarrow x=-\dfrac{2}{3}\)

Answer 3

Điều kiện xác định:$\left\{\begin{matrix} x \neq -1 & \\ x \neq -2 & \\ x \neq -3 & \\ x \neq -4 & \end{matrix}\right.$

Phương trình ban đầu tương đương với:

$\frac{1}{(x+1)(x+2)}+\frac{1}{(x+2)(x+3)}+\frac{1}{(x+3)(x+4)}=\frac{3x-1}{x^2+5x+4}$

$\Leftrightarrow \frac{1}{x+1}-\frac{1}{x+2}+\frac{1}{x+2}-\frac{1}{x+3}+\frac{1}{x+3}-\frac{1}{x+4}=\frac{3x-1}{x^2+5x+4}$

$\Leftrightarrow \frac{1}{x+1}-\frac{1}{x+4}=\frac{3x-1}{(x+1)(x+4)}$

$\Leftrightarrow \frac{3}{(x+1)(x+4)}=\frac{3x-1}{(x+1)(x+4)}\Rightarrow 3=3x-1\Leftrightarrow x=\frac{4}{3}$

Vậy phương trình có tập nghiệm: $S=\left \{ \frac{4}{3} \right \}$