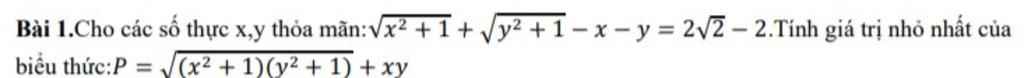Ta có \(P\ge\sqrt{2x.2y}+xy=2\sqrt{xy}+xy\ge1\)
"=" khi \(\left\{{}\begin{matrix}x^2+1=2x\\y^2+1=2y\end{matrix}\right.\Leftrightarrow x=y=1\left(tmgt\right)\)
Min P = 1 khi x = y = 1
Đặt \(\left\{{}\begin{matrix}\sqrt{x^2+1}-x=a>0\\\sqrt{y^2+1}-y=b>0\end{matrix}\right.\)
\(\sqrt{x^2+1}=x+a\Rightarrow x^2+1=x^2+2ax+a^2\)
\(\Rightarrow x=\dfrac{1-a^2}{2a}\), tương tự \(y=\dfrac{1-b^2}{2b}\)
Từ giả thiết: \(2\sqrt{2}-2=a+b\ge2\sqrt{ab}\Rightarrow ab\le3-2\sqrt{2}\)
\(P=\sqrt{\left(\dfrac{a^4-2a^2+1}{4a^2}+1\right)\left(\dfrac{b^4-2b^2+1}{4b^2}+1\right)}+\dfrac{\left(1-a^2\right)\left(1-b^2\right)}{4ab}\)
\(=\sqrt{\left(\dfrac{a^2+1}{2a}\right)^2\left(\dfrac{b^2+1}{2b}\right)^2}+\dfrac{a^2b^2-a^2-b^2+1}{4ab}\)
\(=\dfrac{a^2b^2+a^2+b^2+1}{4ab}+\dfrac{a^2b^2-a^2-b^2+1}{4ab}\)
\(=\dfrac{a^2b^2+1}{2ab}=\dfrac{1}{2}\left(ab+\dfrac{1}{ab}\right)=\dfrac{1}{2}\left(ab+\dfrac{\left(3-2\sqrt{2}\right)^2}{ab}+\dfrac{12\sqrt{2}-16}{ab}\right)\)
\(\ge\dfrac{1}{2}\left[2\sqrt{\dfrac{\left(3-2\sqrt{2}\right)^2ab}{ab}}+\dfrac{12\sqrt{2}-16}{3-2\sqrt{2}}\right]=3\)
\(P_{min}=3\) khi \(a=b=\sqrt{2}-1\Rightarrow x=y=1\)