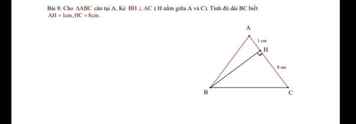
Vì tam giác ABC cân tại A => AB = AC = 9 cm
Theo định lí Pytago tam giác AHB vuông tại H
\(BH=\sqrt{AB^2-AH^2}=4\sqrt{5}\)cm
Theo định lí Pytago tam giác BHC vuông tại H
\(BC=\sqrt{BH^2+HC^2}=12cm\)
Ta có: AC=AH+HC=1+8=9(cm)
Ta có ΔABC cân tại A nên AB=AC=9(cm)
Áp dụng định lý Pi-ta-go vào tam giác vuông AHB ta có:
\(AH^2+HB^2=AB^2\\
\Rightarrow BH^2=AB^2-AH^2\\
\Rightarrow BH=\sqrt{AB^2-AH^2}\\
\Rightarrow BH=\sqrt{9^2-1^2}\\
\Rightarrow BH=4\sqrt{5}\left(cm\right)\)
Áp dụng định lý Pi-ta-go vào tam giác vuông AHC ta có:
\(BH^2+HC^2=BC^2\\ \Rightarrow AC=\sqrt{BH^2+HC^2}\\ \Rightarrow BC=\sqrt{\left(4\sqrt{5}\right)^2+8^2}\\ \Rightarrow BC=12\left(cm\right)\)