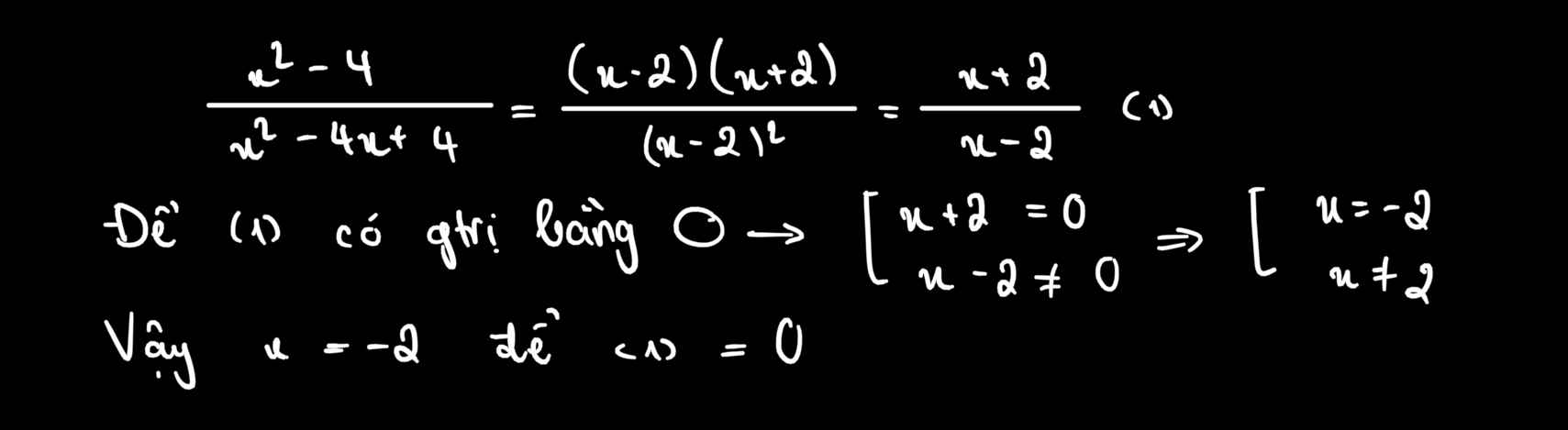Question

Answer 1

\(=\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-2\right)^2}=\dfrac{x+2}{x-2}\)

Để x có giá trị bằng 0 thì \(x\in\left\{2;-2\right\}\)

Answer 2

Answer 3

Để phân thức \(\dfrac{x^2-4}{x^2-4x+4}\) = 0

\(\Rightarrow x^2-4=0\)

\(\Leftrightarrow\left(x+2\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)

Answer 4

để phân thức có giá trị = 0 thì:

\(x^2-4\)=0

=>x=2 hoặc -2

Answer 5

x=2