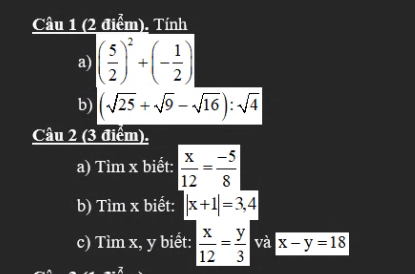Câu 2:
a: \(x=\dfrac{-5\cdot12}{8}=\dfrac{-60}{8}=\dfrac{-15}{2}\)
b: \(\Leftrightarrow\left[{}\begin{matrix}x+1=3.4\\x+1=-3.4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2.4\\x=-4.4\end{matrix}\right.\)
c: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{12}=\dfrac{y}{3}=\dfrac{x-y}{12-3}=\dfrac{18}{9}=2\)
Do đó: x=24; y=6
\(\text{Câu 1:a)}\left(\dfrac{5}{2}\right)^2+\left(-\dfrac{1}{2}\right)\)
\(=\dfrac{25}{4}+\left(-\dfrac{1}{2}\right)=\dfrac{23}{4}\)
\(\text{b)}\left(\sqrt{25}+\sqrt{9}-\sqrt{16}\right):\sqrt{4}\)
\(=\left(5+3-4\right):2\)
\(=4:2=2\)
\(\text{Câu 2:a)}\dfrac{x}{12}=\dfrac{-5}{8}\)
\(\Rightarrow x=\dfrac{12.\left(-5\right)}{8}=\dfrac{-15}{2}\)
\(\text{b)}\left|x+1\right|=3,4\)
\(\left|x+1\right|=\dfrac{17}{5}\)
\(\text{Vậy }x+1=\dfrac{17}{5}\)
\(x\) \(=\dfrac{17}{5}+\left(-1\right)=\dfrac{12}{5}\)
\(\text{hoặc }x+1=\dfrac{-17}{5}\)
\(x\) \(=\left(\dfrac{-17}{5}\right)+\left(-1\right)=\dfrac{-22}{5}\)
\(\Rightarrow x\in\left\{\dfrac{12}{5};\left(\dfrac{-22}{5}\right)\right\}\)
\(\text{c)}\dfrac{x}{12}=\dfrac{y}{3}\text{ và }x-y=18\)
\(\text{Áp dụng tính chất dãy tỉ số bằng nhau:}\)
\(\dfrac{x}{12}=\dfrac{y}{3}=\dfrac{x-y}{12-3}=\dfrac{18}{9}=2\)
\(\Rightarrow x=2.12=24\)
\(y=3.2=6\)