Question

Answer 1

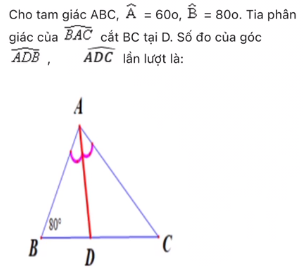
AD là phân giác \(\widehat{A}\) (gt).

\(\Rightarrow\) \(\widehat{BAD} = \) \(\dfrac{1}{2}\)\(\widehat{A}\)  \(=\dfrac{1}{2}.60^o=30^o.\)

Xét \(\Delta ABD:\) 

\(\widehat{BAD} + \widehat{B} + \widehat{ADB}=\) \(180^o\) (Tổng 3 góc trong tam giác).

\(\Rightarrow\) \(\widehat{ADB}=\) \(180^o\) \(-​​​​\widehat{B}- \widehat{BAD}=\) \(180^o-80^o-30^o=70^o.\)

Mà \(\widehat{ADB}+\widehat{ADC}=\) \(180^o\) (kề bù).

\(\Rightarrow\) \(​​\widehat{ADB}=\) \(110^o.\)

Answer 2

\(\widehat{ACB}=40^0\)

\(\widehat{BAD}=\widehat{CAD}=\dfrac{1}{2}\cdot60^0=30^0\)

\(\widehat{ADB}=180^0-\left(80^0+30^0\right)=70^0\)

\(\widehat{ADC}=180^0-70^0=110^0\)