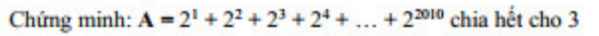\(A=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{2009}\left(1+2\right)=2.3+2^3.3+...+2^{2009}.3=3\left(2+2^3+....+2^{2009}\right)⋮3\)
\(A=2^1+2^2+2^3+2^4+...+2^{2010}\)
\(\Rightarrow A=\left(2^1+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{2009}+2^{2010}\right)\)
\(\Rightarrow A=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{2009}\left(1+2\right)\)
\(\Rightarrow A=\left(1+2\right)\left(2+2^3+...+2^{2009}\right)\)
\(\Rightarrow A=3\left(2+2^3+...+2^{2009}\right)3⋮\)
\(A=2^1+2^2+2^3+...+2^{2010}\)
\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{2009}+2^{2010}\right)\)
\(A=\left(2+2^2\right)+2^2\left(2+2^2\right)+...+2^{2008}\left(2+2^2\right)\)
\(A=\left(2+2^2\right)\left(1+2^2+...+2^{2008}\right)\)
mà \(2+2^2⋮3\) \(\Rightarrow\left(2+2^2\right)\left(1+2^2+...+2^{2008}\right)⋮3\)
hay \(A=2^1+2^2+2^3+...+2^{2010}\) chia hết cho 3