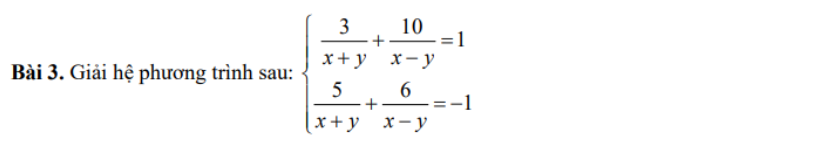Đặt: \(\left[{}\begin{matrix}a=\dfrac{1}{x+y}\\b=\dfrac{1}{x-y}\end{matrix}\right.\)
\(=>\left\{{}\begin{matrix}3a+10b=1\\5a+6b=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}15a+50b=5\\15a+18b=-3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}32b=8\\15a+50b=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{1}{4}\\15a+50\cdot\dfrac{1}{4}=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{1}{4}\\a=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}a=\dfrac{1}{x+y}=-\dfrac{1}{2}\\b=\dfrac{1}{x-y}=\dfrac{1}{4}\end{matrix}\right.\) Tới đây chắc bạn tự giải x và y được rồi chứ nhỉ :)?
\(ĐK:x+y\ne0;x-y\ne0\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{15}{x+y}+\dfrac{50}{x-y}=5\\\dfrac{15}{x+y}+\dfrac{18}{x-y}=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{32}{x-y}=8\\\dfrac{3}{x+y}+\dfrac{10}{x-y}=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x-y=4\\\dfrac{3}{x+y}+\dfrac{10}{4}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y+4\\\dfrac{3}{2y+4}=-\dfrac{3}{2}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=y+4\\2y+4=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y+4=-3+4=1\\y=-3\end{matrix}\right.\left(tm\right)\)
Vậy \(\left(x;y\right)=\left(1;-3\right)\)