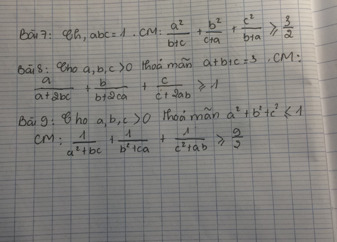Bài 7: Bổ sung điều kiện a,b,c dương nha b
Áp dụng BĐT cosi:
\(\dfrac{a^2}{b+c}+\dfrac{b+c}{4}\ge2\sqrt{\dfrac{a^2\left(b+c\right)}{4\left(b+c\right)}}=a\)
CMTT: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{b^2}{c+a}+\dfrac{c+a}{4}\ge b\\\dfrac{c^2}{a+b}+\dfrac{a+b}{4}\ge c\end{matrix}\right.\)
Cộng VTV
\(\Leftrightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}+\dfrac{2\left(a+b+c\right)}{4}\ge a+b+c\\ \Leftrightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge\dfrac{2\left(a+b+c\right)-\left(a+b+c\right)}{2}=\dfrac{a+b+c}{2}\\ \Leftrightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge\dfrac{3\sqrt[3]{abc}}{2}=\dfrac{3\cdot1}{2}=\dfrac{3}{2}\)
Dấu \("="\Leftrightarrow a=b=c=1\)