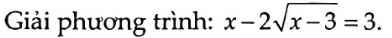\(ĐK:x\ge3\\ PT\Leftrightarrow2\sqrt{x-3}=x-3\\ \Leftrightarrow4x-12=x^2-6x+9\\ \Leftrightarrow x^2-10x+21=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=7\left(tm\right)\end{matrix}\right.\)
\(x-2\sqrt{x-3}=3\)
⇒ \(2\sqrt{x-3}=x-3\)
⇒ \(\left(2\sqrt{x-3}\right)^2=\left(x-3\right)^2\)
⇒ \(4\left(x-3\right)=x^2-6x+9\)
⇒ \(4x-12=x^2-6x+9\)
⇒ \(4x-x^2+6x=9+12\)
⇒ \(x^2+2x=21\)
⇒ \(\left(x+1\right)^2=22\)
⇒ \(\left[{}\begin{matrix}x+1=\sqrt{22}\\x+1=-\sqrt{22}\end{matrix}\right.\)
⇒ \(\left[{}\begin{matrix}x=\sqrt{22}-1\\x=-\sqrt{22}-1\end{matrix}\right.\)