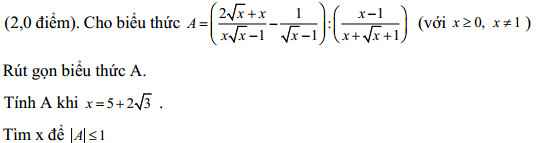\(a,A=\dfrac{2\sqrt{x}+x-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ A=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)}=\dfrac{1}{x-1}\)
\(b,A=\dfrac{1}{5+2\sqrt{3}-1}=\dfrac{1}{4+2\sqrt{3}}=\dfrac{4-2\sqrt{3}}{4}=\dfrac{2-\sqrt{3}}{2}\)
\(c,\left|A\right|\le1\Leftrightarrow-1\le A\le1\Leftrightarrow-1\le\dfrac{1}{x-1}\le1\)
Xét \(\dfrac{1}{x-1}\ge-1\Leftrightarrow\dfrac{x}{x-1}\ge0\Leftrightarrow\left[{}\begin{matrix}x>1\\x\le0\end{matrix}\right.\)
Xét \(\dfrac{1}{x-1}\le1\Leftrightarrow\dfrac{2-x}{x-1}\le0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}2-x\le0\\x-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}2-x\ge0\\x-1< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\ge2\\x< 1\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x\ge2\\x\le0\end{matrix}\right.\) thỏa đề bài