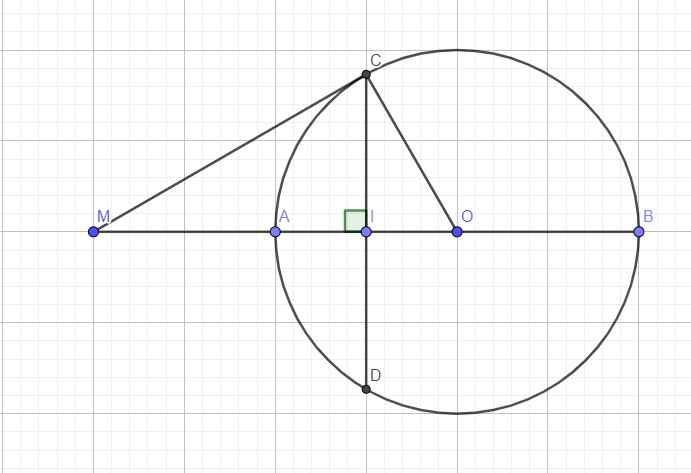
Đặt \(AB=2R\Rightarrow OA=OC=R\Rightarrow\left\{{}\begin{matrix}OM=2OA=2R\\OI=\dfrac{1}{2}OA=\dfrac{1}{2}R\end{matrix}\right.\)
\(\Rightarrow\dfrac{OI}{OC}=\dfrac{OC}{OM}=\dfrac{1}{2}\)
Xét hai tam giác OCI và OMC có:
\(\left\{{}\begin{matrix}\dfrac{OI}{OC}=\dfrac{OC}{OM}\\\widehat{MOC\text{ chung}}\end{matrix}\right.\) \(\Rightarrow\Delta OCI\sim\Delta OMC\)
\(\Rightarrow\widehat{OCM}=\widehat{OIC}=90^0\)
\(\Rightarrow OC\perp MC\) hay MC là tiếp tuyến của đường tròn
Đúng 0
Bình luận (0)
