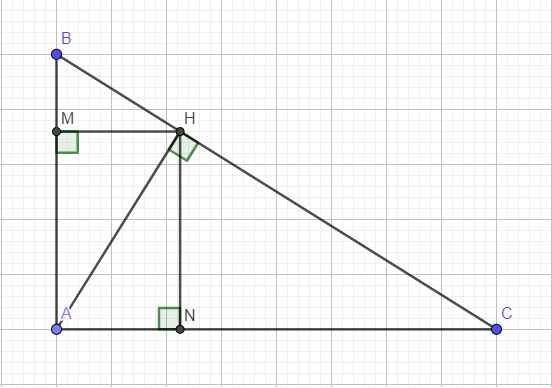
a.
Áp dụng hệ thức lượng trong tam giác vuông ABH với đường cao HM:
\(AH^2=AM.AB\)
Hệ thức lượng trong tam giác vuông CAH:
\(AH^2=AN.AC\)
\(\Rightarrow AM.AB=AN.AC\)
b.
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=4,8\left(cm\right)\)
\(AH^2=AM.AB\Rightarrow AM=\dfrac{AH^2}{AB}=3,84\left(cm\right)\)
c.
Ta có \(\widehat{AHN}=\widehat{C}\) (cùng phụ \(\widehat{HAC}\)) \(\Rightarrow cos\widehat{AHN}=cos\widehat{C}=\dfrac{AC}{BC}\)
\(HN||AB\) (cùng vuông góc AC) \(\Rightarrow\widehat{NHC}=\widehat{B}\) (đồng vị)
\(\Rightarrow cos\widehat{NHC}=cos\widehat{B}=\dfrac{AB}{BC}\)
\(\Rightarrow cos\widehat{AHN}+cos\widehat{NHC}=\dfrac{AB+AC}{BC}>\dfrac{BC}{BC}=1\) (đpcm)
(\(AB+AC>BC\) là bất đẳng thức tam giác của lớp 7)