1.
\(x=1\) là tiệm cận đứng \(\Rightarrow n=1\)
\(y=-3;y=3\) là 2 tiệm cận ngang \(\Rightarrow m=9\)
\(\Rightarrow mn< 0\) là mệnh đề sai
2.
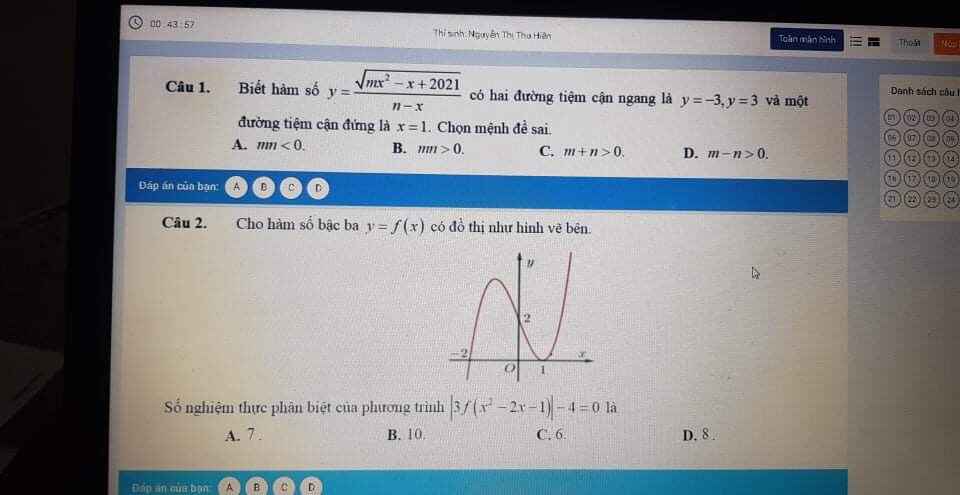
\(x^2-2x-1=\left(x-1\right)^2-2\ge-2\) với mọi x
\(\Rightarrow f\left(x^2-2x-1\right)\ge0\) với mọi x
Do đó pt trở thành:
\(3f\left(x^2-2x-1\right)-4=0\Leftrightarrow f\left(x^2-2x-1\right)=\dfrac{4}{3}\) có 3 nghiệm
\(\Rightarrow\) Phương trình đã cho có 6 nghiệm