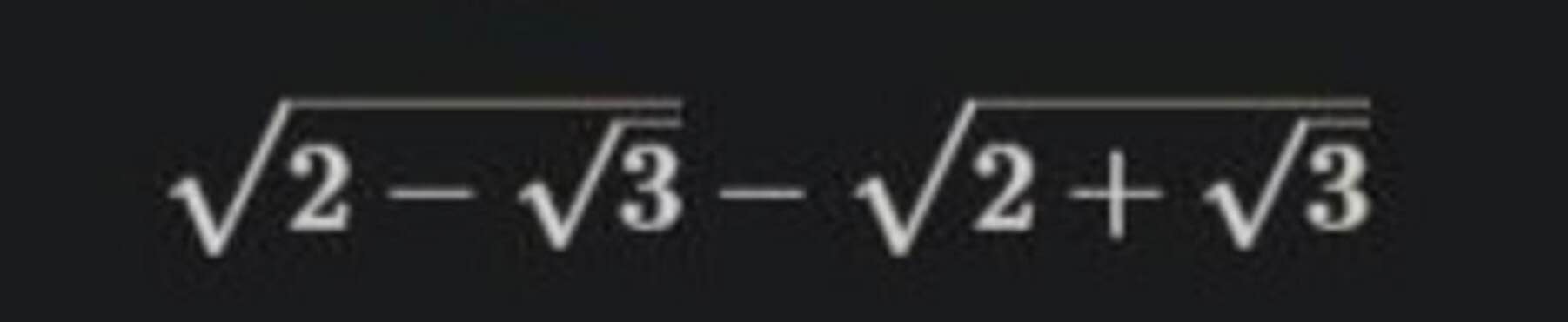\(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)
\(=\dfrac{\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}}{\sqrt{2}}\)
\(=\dfrac{\sqrt[]{3}-1-\sqrt{3}-1}{\sqrt{2}}=\dfrac{-2}{\sqrt{2}}=-\sqrt{2}\)
Đặt \(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}=A\)
⇒\(A^2=\left(\sqrt{2-\sqrt{3}}+\left(-\sqrt{2+\sqrt{3}}\right)\right)^2\)
Áp dụng BĐT B.C.S ta có
\(\left(\sqrt{2-\sqrt{3}}+\left(-\sqrt{2+\sqrt{3}}\right)\right)^2\)\(\text{≤}\left(1^2+1^2\right)\left(2-\sqrt{3}+2+\sqrt{3}\right)\)
\(=2.4=8\)
⇒\(A^2\text{≤}8\)
⇒\(A\text{≤}2\sqrt{3}\)