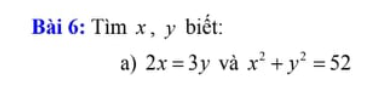\(2x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{2}\Rightarrow\dfrac{x^2}{9}=\dfrac{y^2}{4}\)
Áp dụng t/c dtsbn:
\(\dfrac{x^2}{9}=\dfrac{y^2}{4}=\dfrac{x^2+y^2}{9+4}=\dfrac{52}{13}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x^2=4.9=36\\y^2=4.4=16\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=6\\y=4\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=-4\end{matrix}\right.\end{matrix}\right.\)
a: \(2x=3y\)
nên \(\dfrac{x}{3}=\dfrac{y}{2}\)
Đặt \(\dfrac{x}{3}=\dfrac{y}{2}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k\\y=2k\end{matrix}\right.\)
\(x^2+y^2=52\)
\(\Leftrightarrow13k^2=52\)
\(\Leftrightarrow k^2=4\)
Trường hợp 1: k=2
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=6\\y=2k=4\end{matrix}\right.\)
Trường hợp 2: k=-2
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=-6\\y=2k=-4\end{matrix}\right.\)