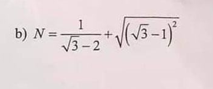\(N=\dfrac{\sqrt{3}+2}{-1}+\sqrt{3}-1=-\sqrt{3}-2+\sqrt{3}-1=-3\)
N = \(\dfrac{1}{\sqrt{3}-2}+\left(\sqrt{3}-1\right)=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}-2\right)+1}{\sqrt{3}-2}\)
= \(\dfrac{5-3\sqrt{3}+1}{\sqrt{3}-2}=\dfrac{6-3\sqrt{3}}{\sqrt{3}-2}=-3\)
\(N=\dfrac{-\left(2+\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}+\sqrt{3}-1\)
\(N=-2-\sqrt{3}+\sqrt{3}-1=-3\)
\(N=\dfrac{1}{\sqrt{3}-2}+\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=\dfrac{1}{\sqrt{3}-2}+\left(\sqrt{3}-2\right)+1\)
Áp dụng BĐT cô si ta có:
\(\dfrac{1}{\sqrt{3}-2}+\left(\sqrt{3}-2\right)\) ≥ \(2\sqrt{\dfrac{1}{\sqrt{3}-2}.\left(\sqrt{3}-2\right)}+1\)\(=3\)