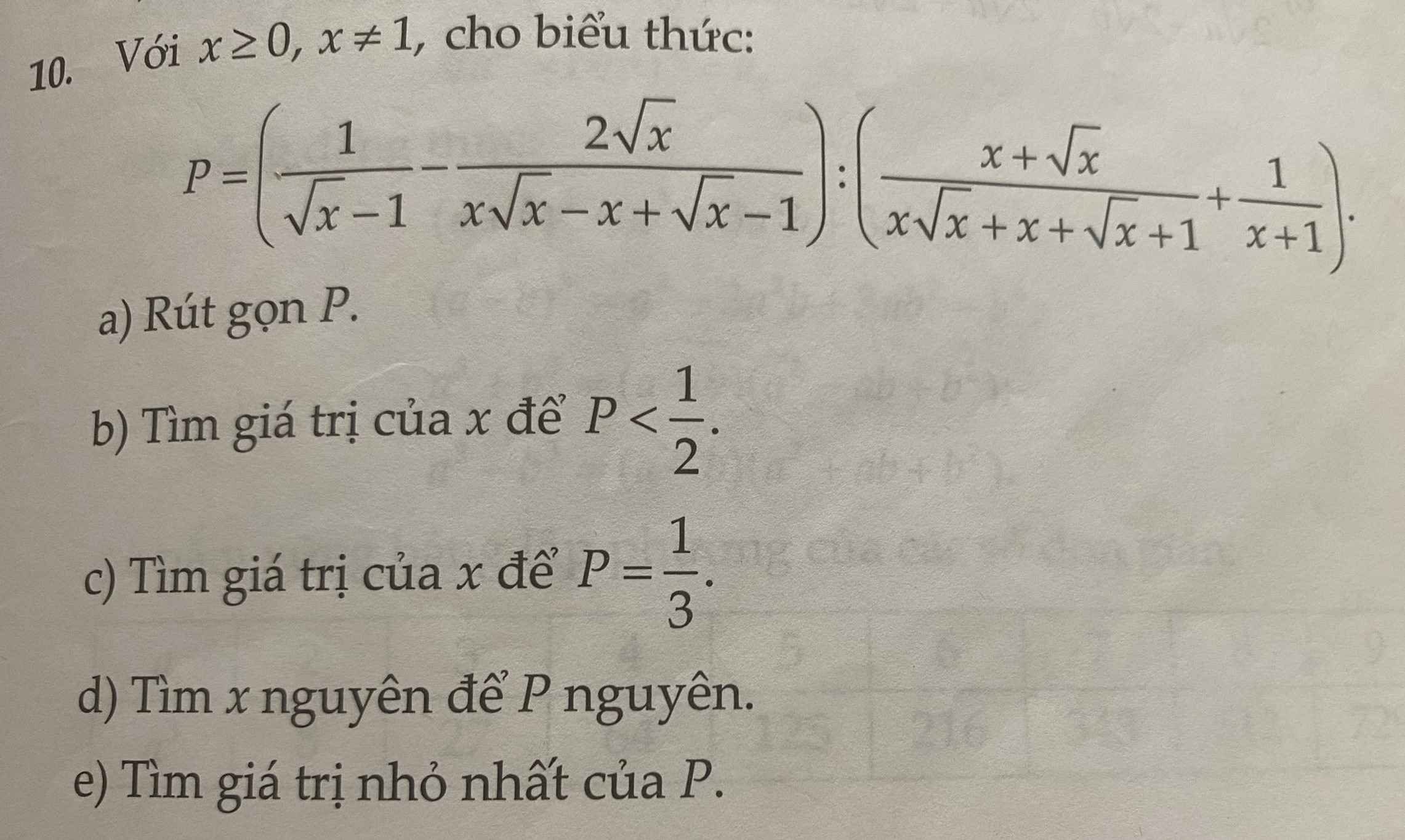a. \(P=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{x\sqrt{x}-x+\sqrt{x}-1}\right):\left(\dfrac{x+\sqrt{x}}{x\sqrt{x}+x+\sqrt{x}+1}+\dfrac{1}{x+1}\right)\)
\(=\dfrac{x+1-2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}:\dfrac{x+\sqrt{x}+\sqrt{x}+1}{\left(x+1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(x+1\right)\left(\sqrt{x}-1\right)}.\dfrac{\left(x+1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
b. Để \(P< \dfrac{1}{2}\) thì \(\dfrac{\sqrt{x}-3}{\sqrt{x}+1}< \dfrac{1}{2}\) \(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{1}{2}< 0\) \(\Leftrightarrow\dfrac{\sqrt{x}-3}{2\left(\sqrt{x}+1\right)}< 0\)
mà \(2\left(\sqrt{x}+1\right)\ge2>0\forall x\) \(\Rightarrow\sqrt{x}-3< 0\Rightarrow\sqrt{x}< 3\Leftrightarrow x< 9\)
c. Để \(P=\dfrac{1}{3}\) thì\(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{1}{3}\Rightarrow3\left(\sqrt{x}-1\right)=\sqrt{x}+1\Rightarrow2\sqrt{x}=4\Rightarrow\sqrt{x}=2\Rightarrow x=4\)
d. Ta có \(P=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1-2}{\sqrt{x}+1}=1-\dfrac{2}{\sqrt{x}+1}\)
Để \(P\) nhận giá trị nguyên thì \(2⋮\left(\sqrt{x}+1\right)\Rightarrow\left(\sqrt{x}+1\right)\inƯ\left(2\right)\)
\(\Rightarrow\sqrt{x}+1\in\left\{1;-1;2;-2\right\}\) \(\Rightarrow x\in\left\{0;1\right\}\)
e. Ta có \(P=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=1-\dfrac{2}{\sqrt{x}+1}\)
Với mọi \(x\ge0\) thì \(\sqrt{x}\ge0\) \(\Rightarrow\sqrt{x}+1\ge1\Rightarrow\dfrac{2}{\sqrt{x}+1}\le2\Rightarrow P=1-\dfrac{2}{\sqrt{x}+1}\ge-1\)
Dấu "=" xảy ra khi \(\sqrt{x}+1=1\Leftrightarrow\sqrt{x}=0\Leftrightarrow x=0\)
Vậy \(P_{min}=-1\) khi \(x=0\)