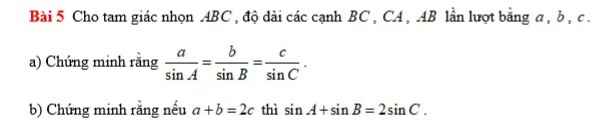a) Kẻ đường cao AH và BK của tam giác ABC
Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông ABK,
\(\dfrac{c}{sinC}=AB:\dfrac{AH}{AC}=\dfrac{AC.AB}{AH}\)
\(\dfrac{b}{sinB}=AC:\dfrac{AH}{AB}=\dfrac{AC.AB}{AH}\)
\(\Rightarrow\dfrac{c}{sinC}=\dfrac{b}{sinB}\left(1\right)\)
\(\dfrac{a}{sinA}=BC:\dfrac{BK}{AB}=\dfrac{AB.BC}{BK}\)
\(\dfrac{c}{sinC}=AB:\dfrac{BK}{BC}=\dfrac{AB.BC}{BK}\)
\(\Rightarrow\dfrac{a}{sinA}=\dfrac{c}{sinC}\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrowđpcm\)
Đúng 0
Bình luận (0)
