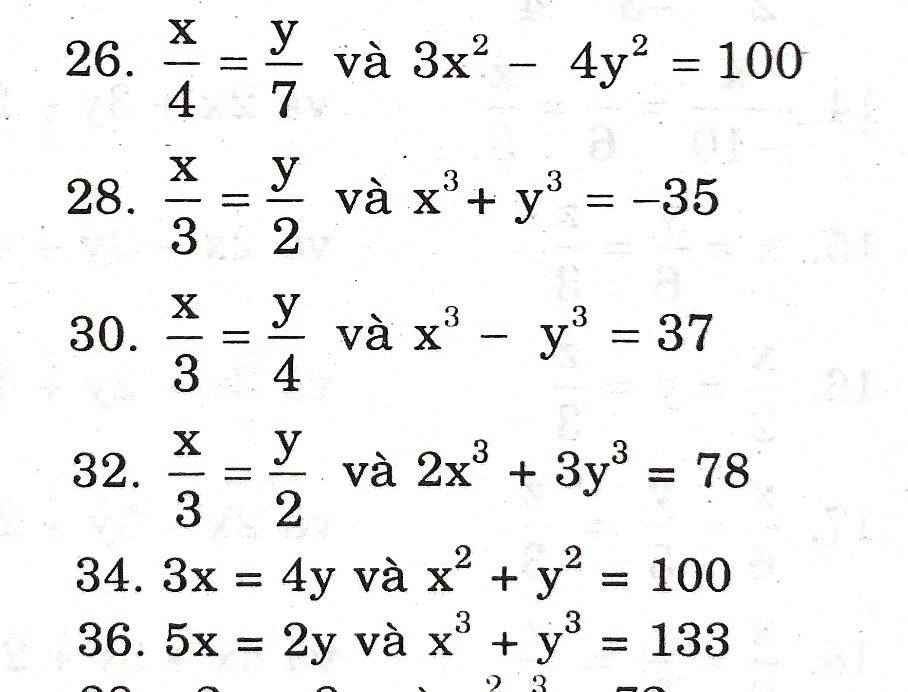34: Ta có: 3x=4y
\(\Leftrightarrow\dfrac{x}{4}=\dfrac{y}{3}\)
Đặt \(\dfrac{x}{4}=\dfrac{y}{3}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k\\y=3k\end{matrix}\right.\)
Ta có: \(x^2+y^2=100\)
\(\Leftrightarrow25k^2=100\)
\(\Leftrightarrow k^2=4\)
Trường hợp 1: k=2
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=8\\y=3k=6\end{matrix}\right.\)
Trường hợp 2: k=-2
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=-8\\y=3k=-6\end{matrix}\right.\)
26.\(x=\dfrac{4}{7}y\Rightarrow3\left(\dfrac{4}{7}y\right)^2-4y^2=100\Rightarrow\\ -\dfrac{148}{49}y^2=100\left(vôlí\right)\Rightarrow vôn_{\delta}\)
28.\(x=\dfrac{3}{2}y\Rightarrow\left(\dfrac{3}{2}y\right)^3+y^3=-35\Rightarrow y=-2\Rightarrow x=-3\)
30.\(x=\dfrac{3}{4}y\Rightarrow\left(\dfrac{3}{4}y\right)^3-y^3=37\Rightarrow y=-4\Rightarrow x=-3\)
32.\(x=\dfrac{3}{2}y\Rightarrow2\left(\dfrac{3}{2}y\right)^3+3y^3=78\Rightarrow y=2\Rightarrow x=3\)
34.\(x=\dfrac{3}{4}y\Rightarrow2\left(\dfrac{3}{4}y\right)^2+y^2=100\Rightarrow\left[{}\begin{matrix}y=6\\y=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right.\)
36.\(x=\dfrac{2}{5}y\Rightarrow\left(\dfrac{2}{5}y\right)^3+y^3=133\Rightarrow y=5\Rightarrow x=2\)
30: Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k\\y=4k\end{matrix}\right.\)
Ta có: \(x^3-y^3=37\)
\(\Leftrightarrow27k^3-64k^3=37\)
\(\Leftrightarrow k^3=-1\)
hay k=-1
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=-3\\y=4k=-4\end{matrix}\right.\)