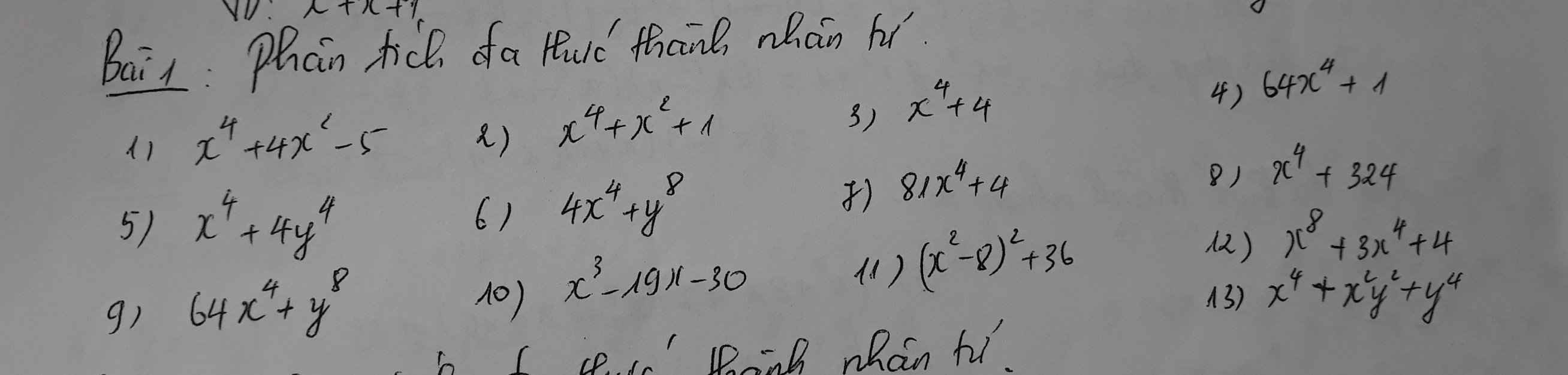1: \(x^4+4x^2-5\)
\(=\left(x^2+5\right)\left(x^2-1\right)\)
\(=\left(x^2+5\right)\left(x-1\right)\left(x+1\right)\)
2: \(x^4+x^2+1\)
\(=\left(x^2+1\right)^2-x^2\)
\(=\left(x^2-x+1\right)\left(x^2+x+1\right)\)
3: \(x^4+4\)
\(=\left(x^2+2\right)^2-4x^2\)
\(=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\)
4: \(64x^4+1\)
\(=\left(8x^2+1\right)^2-16x^2\)
\(=\left(8x^2-4x+1\right)\left(8x^2+4x+1\right)\)
5: \(x^4+4y^4\)
\(=\left(x^2+2y^2\right)^2-4x^2y^2\)
\(=\left(x^2-2xy+2y^2\right)\left(x^2+2xy+2y^2\right)\)+
7: \(81x^4+4\)
\(=\left(9x^2+2\right)^2-36x^2\)
\(=\left(9x^2-6x+2\right)\left(9x^2+6x+2\right)\)
8: Ta có: \(x^4+324\)
\(=\left(x^2+18\right)^2-36x^2\)
\(=\left(x^2-6x+18\right)\left(x^2+6x+18\right)\)
10: Ta có: \(x^3-19x-30\)
\(=x^3-5x^2+5x^2-25x+6x-30\)
\(=x^2\left(x-5\right)+5x\left(x-5\right)+6\left(x-5\right)\)
\(=\left(x-5\right)\left(x^2+5x+6\right)\)
\(=\left(x-5\right)\left(x+2\right)\left(x+3\right)\)
11: Ta có: \(\left(x^2-8\right)^2+36\)
\(=x^4-16x^2+64+36\)
\(=x^4-16x^2+100\)
\(=x^4+20x^2+100-36x^2\)
\(=\left(x^2-6x+10\right)\left(x^2+6x+10\right)\)