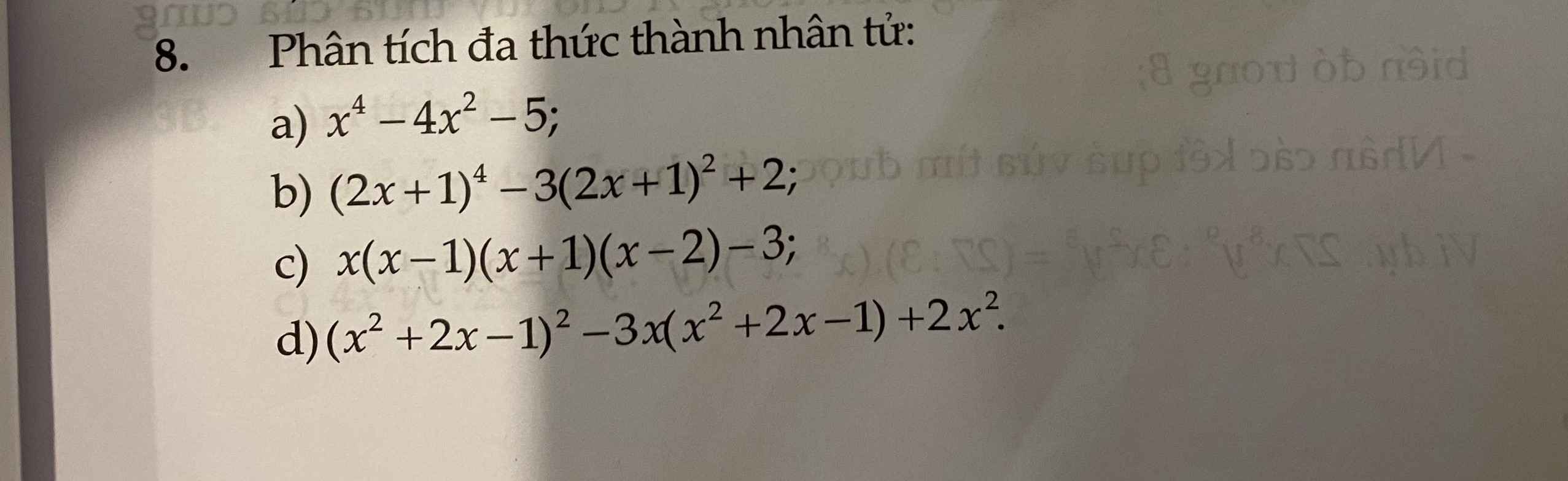a: Ta có: \(x^4-4x^2-5\)
\(=x^4-5x^2+x^2-5\)
\(=\left(x^2-5\right)\left(x^2+1\right)\)
b: Ta có: \(\left(2x+1\right)^4-3\left(2x+1\right)^2+2\)
\(=\left(2x+1\right)^4-2\left(2x+1\right)^2-\left(2x+1\right)^2+2\)
\(=\left(2x+1\right)^2\left[\left(2x+1\right)^2-2\right]-\left[\left(2x+1\right)^2-2\right]\)
\(=\left(4x^2+4x+1-2\right)\left(2x+1-1\right)\left(2x+1+1\right)\)
\(=4x\left(x+1\right)\left(4x^2+4x-1\right)\)
c) Ta có: \(x\left(x-1\right)\left(x+1\right)\left(x-2\right)-3\)
\(=\left(x^2-x\right)\left(x^2-x-2\right)-3\)
\(=\left(x^2-x\right)^2-2\left(x^2-x\right)-3\)
\(=\left(x^2-x\right)^2-3\left(x^2-x\right)+\left(x^2-x\right)-3\)
\(=\left(x^2-x\right)\left(x^2-x-3\right)+\left(x^2-x-3\right)\)
\(=\left(x^2-x-3\right)\left(x^2-x+1\right)\)