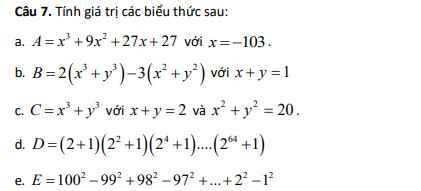a.
$A=x^3+9x^2+27x+27=(x+3)^3=(-103+3)^3=(-100)^3=-1000000$
b.
$B=2(x^3+y^3)-3(x^2+y^2)$
$=2[(x+y)^3-3xy(x+y)]-3[(x+y)^2-2xy]$
$=2(1-3xy)-3(1-2xy)=2-6xy-3+6xy=-1$
a) Ta có: \(A=x^3+9x^2+27x+27\)
\(=x^3+3\cdot x^2\cdot3+3\cdot x\cdot3^2+3^3\)
\(=\left(x+3\right)^3\)
\(=\left(-100\right)^3=-1000000\)
b) Ta có: \(A=2\left(x^3+y^3\right)-3\left(x^2+y^2\right)\)
\(=2\left[\left(x+y\right)^3-3xy\left(x+y\right)\right]-3\left(x+y\right)^2+6xy\)
\(=2\left(x+y\right)^3-3\left(x+y\right)^2-6xy\left(x+y\right)+6xy\)
\(=\left(x+y\right)^2\cdot\left[2\left(x+y\right)-3\right]-6xy\left(x+y-1\right)\)
\(=1^2\cdot\left(2\cdot1-3\right)\)
\(=-1\)
c) Ta có: \(x+y=2\)
\(\Leftrightarrow\left(x+y\right)^2=4\)
\(\Leftrightarrow x^2+y^2+2xy=4\)
\(\Leftrightarrow2xy=-16\)
hay xy=-8
Ta có: \(C=x^3+y^3\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=2\cdot\left(20+8\right)\)
=56
c.
$xy=\frac{(x+y)^2-(x^2+y^2)}{2}=\frac{2^2-20}{2}=-8$
$C=x^3+y^3=(x+y)^3-3xy(x+y)=2^3-3(-8).2=56$
d.
$D=(2+1)(2^2+1)(2^4+1)...(2^{64}+1)$
$=(2-1)(2+1)(2^2+1)(2^4+1)...(2^{64}+1)$
$=(2^2-1)(2^2+1)(2^4+1)....(2^{64}+1)$
$=(2^4-1)(2^4+1)....(2^{64}+1)$
$=(2^8-1)(2^8+1)....(2^{64}+1)$
$=(2^{16}-1)(2^{16}+1)....(2^{64}+1)$
$=(2^{32}-1)(2^{32}+1)(2^{64}+1)$
$=(2^{64}-1)(2^{64}+1)=2^{128}-1$
e.
$E=100^2-99^2+98^2-97^2+....+2^2-1$
$=(100^2-99^2)+(98^2-97^2)+...+(2^2-1)$
$=(100-99)(100+99)+(98-97)(98+97)+...+(2-1)(2+1)$
$=199+195+191+...+3$
$=[\frac{199-3}{4}+1].\frac{199+3}{2}=5050$
d) Ta có: \(D=\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)\cdot...\cdot\left(2^{64}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\cdot...\cdot\left(2^{64}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\cdot...\cdot\left(2^{64}+1\right)\)
\(=\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)\cdot...\cdot\left(2^{64}+1\right)\)
\(=\left(2^{16}-1\right)\left(2^{16}+1\right)\left(2^{32}+1\right)\left(2^{64}+1\right)\)
\(=\left(2^{32}-1\right)\left(2^{32}+1\right)\left(2^{64}+1\right)\)
\(=\left(2^{64}-1\right)\left(2^{64}+1\right)\)
\(=2^{128}-1\)
e) Ta có: \(E=100^2-99^2+98^2-97^2+...+2^2-1^2\)
\(=100+99+98+97+...+2+1\)
=5050