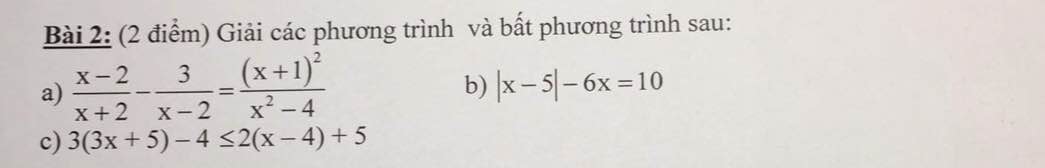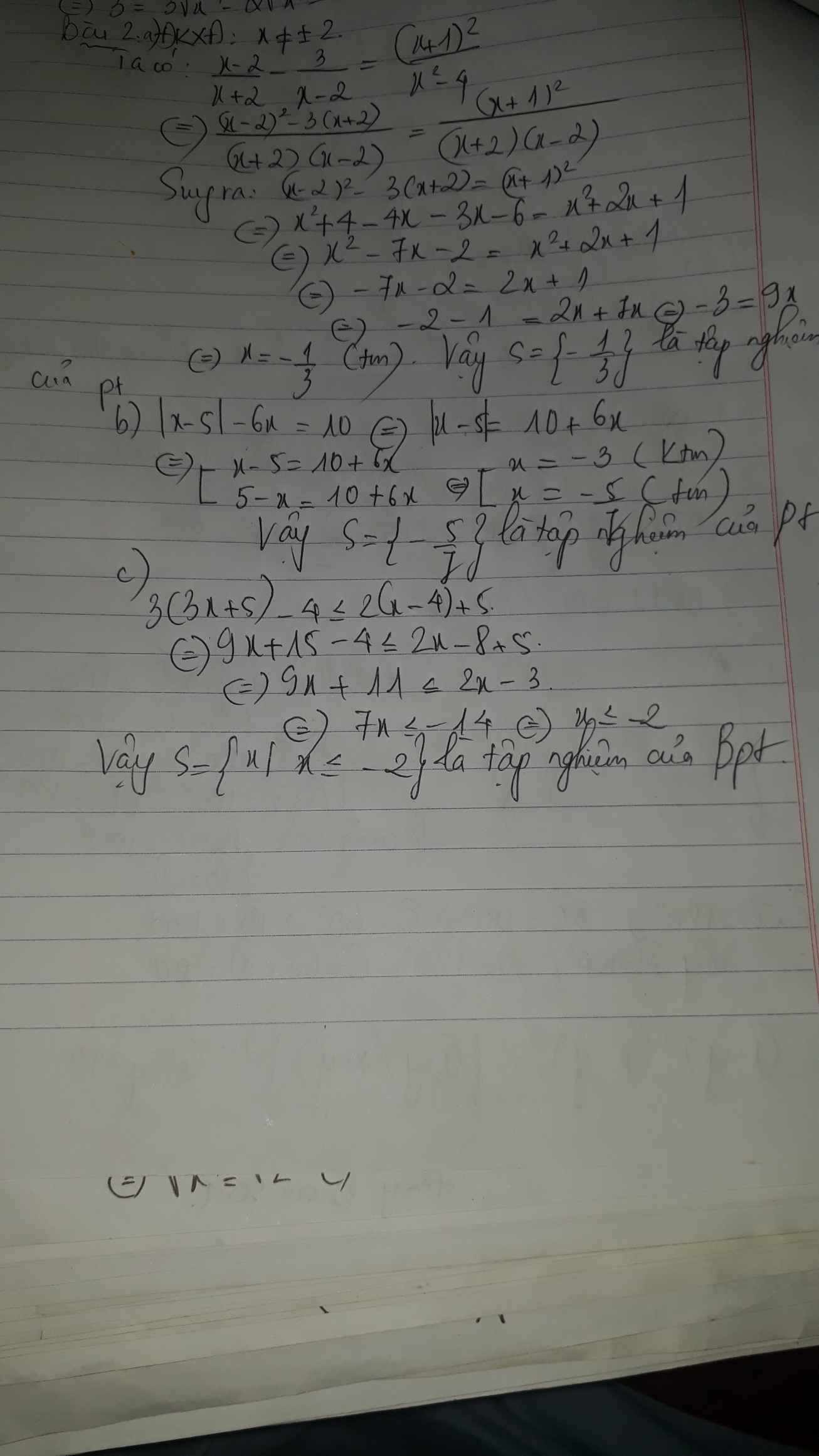Bài 2 :
a) \(\dfrac{x-2}{x+2}-\dfrac{3}{x-2}=\dfrac{\left(x+1\right)^2}{x^2-4}\)
\(\dfrac{x-2}{x+2}-\dfrac{3}{x-2}=\dfrac{\left(x+1\right)^2}{\left(x-2\right)\left(x+2\right)}\)
dkxd : x ≠ -2
x ≠ 2
MTC : (x - 2)(x + 2)
Quy đồng mẫu thức hai vế của phương trình :
⇒ \(\dfrac{\left(x-2\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\) = \(\dfrac{\left(x+1\right)^2}{\left(x-2\right)\left(x+2\right)}\)
Suy ra : (x - 2)(x - 2) - 3(x + 2) = (x + 1)2
\(\Leftrightarrow\) (x - 2)2 - 3(x + 2) = (x + 1)2
\(\Leftrightarrow\) x2 - 4x + 4 - 3x - 6 = x2 + 2x + 1
\(\Leftrightarrow\) x2 - 4x + 4 - 3x - 6 - x2 - 2x - 1 = 0
\(\Leftrightarrow\) -9x - 3 = 0
\(\Leftrightarrow\) -9x = 3
\(\Leftrightarrow\) x = \(-\dfrac{3}{9}=-3\) (thỏa mãn)
Vậy S = \(\left\{-3\right\}\)
b) \(\left|x-5\right|-6x=10\)
\(\left|x-5\right|\) = x - 5 nếu x - 5 ≥ 0
\(\Leftrightarrow\) x ≥ 5
\(\left|x-5\right|\) = -(x - 5) nếu x - 5 < 0
\(\Leftrightarrow\) x < 5
Nếu x ≥ 5 thì phương trình viết được
x - 5 - 6x = 10
\(\Leftrightarrow\) x - 5 - 6x - 10 = 0
\(\Leftrightarrow\) -5x - 15 = 0
\(\Leftrightarrow\) -5x = 15
\(\Leftrightarrow\) x = \(-\dfrac{15}{5}=-3\) (không thỏa mãn x ≥ 5)
Nếu x < 5 thì phương trình viết được
-(x - 5) - 6x = 10
\(\Leftrightarrow\) -x + 5 - 6x - 10
\(\Leftrightarrow\) -7x - 5 = 0
\(\Leftrightarrow\) -7x = 5
\(\Leftrightarrow\) x = \(-\dfrac{5}{7}\) (thỏa mãn x < 5)
Vậy bất phương trình có nghiệm là : x = \(-\dfrac{5}{7}\)
c) 3(3x + 5) - 4 ≤ 2(x - 4) + 5
\(\Leftrightarrow\) 9x + 15 - 4 ≤ 2x - 8 + 5
\(\Leftrightarrow\) 9x - 2x ≤ -8 + 5 - 15 + 4
\(\Leftrightarrow\) 5x ≤ -14
\(\Leftrightarrow\) x ≤ \(-\dfrac{14}{5}\)
Chúc bạn học tốt
a) Ta có: \(\dfrac{x-2}{x+2}-\dfrac{3}{x-2}=\dfrac{\left(x+1\right)^2}{x^2-4}\)
\(\Leftrightarrow x^2-4x+4-3\left(x+2\right)=\left(x+1\right)^2\)
\(\Leftrightarrow x^2-4x+4-3x-6-x^2-2x-1=0\)
\(\Leftrightarrow-9x-3=0\)
\(\Leftrightarrow-9x=3\)
hay \(x=-\dfrac{1}{3}\)
b) Ta có: \(\left|x-5\right|-6x=10\)
\(\Leftrightarrow\left|x-5\right|=6x+10\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=6x+10\left(x\ge5\right)\\5-x=6x+10\left(x< 5\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-6x=10+5\\-x-6x=10-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\left(loại\right)\\x=\dfrac{-5}{7}\left(nhận\right)\end{matrix}\right.\)