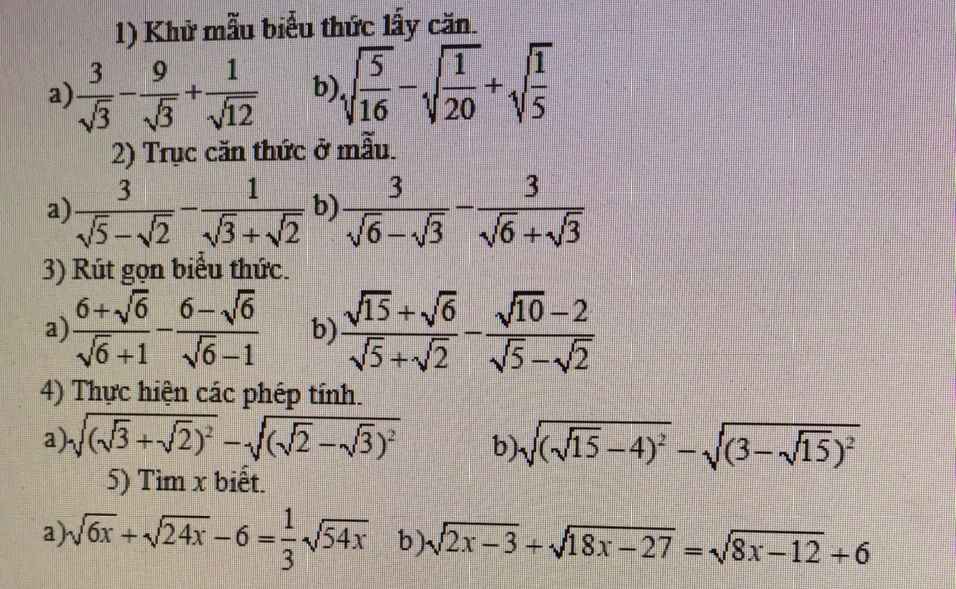4)a)\(=\left|\sqrt{3}+\sqrt{2}\right|-\left|\sqrt{2}-\sqrt{3}\right|\)
\(=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}\left(do\sqrt{3}>\sqrt{2}\right)\)
\(=2\sqrt{2}\)
b)\(=\left|\sqrt{15}-4\right|-\left|3-\sqrt{15}\right|\)
\(=4-\sqrt{15}-\sqrt{15}+3\) (do \(4>\sqrt{15}>3\))
\(=7-2\sqrt{15}\)
Bài nào đây bạn ?
P/s; Chỉ đc hỏi 1 bài thôi nhé!
1.
a. \(=\frac{3\sqrt{3}}{3}-\frac{9\sqrt{3}}{3}+\frac{1}{2\sqrt{3}}=\sqrt{3}-3\sqrt{3}+\frac{\sqrt{3}}{6}=-2\sqrt{3}+\frac{\sqrt{3}}{6}\)
\(=\frac{-12\sqrt{3}+\sqrt{3}}{6}=\frac{-11\sqrt{3}}{6}\)
b. \(=\sqrt{\frac{5}{16}}-\sqrt{\frac{5}{100}}+\sqrt{\frac{5}{25}}=\frac{\sqrt{5}}{4}-\frac{\sqrt{5}}{10}+\frac{\sqrt{5}}{5}\)
\(=\frac{5\sqrt{5}-2\sqrt{5}+4\sqrt{5}}{20}=\frac{7\sqrt{5}}{20}\)
2.
a.
\(=\frac{3(\sqrt{5}+\sqrt{2})}{(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})}-\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}\)
\(=\frac{3(\sqrt{5}+\sqrt{2})}{5-2}-\frac{\sqrt{3}-\sqrt{2}}{3-2}=\sqrt{5}+\sqrt{2}-(\sqrt{3}-\sqrt{2})=\sqrt{5}-\sqrt{3}+2\sqrt{2}\)
b.
\(=\frac{3(\sqrt{6}+\sqrt{3})}{(\sqrt{6}-\sqrt{3})(\sqrt{6}+\sqrt{3})}-\frac{3(\sqrt{6}-\sqrt{3})}{(\sqrt{6}-\sqrt{3})(\sqrt{6}+\sqrt{3})}\)
\(=\frac{3(\sqrt{6}+\sqrt{3})}{6-3}-\frac{3(\sqrt{6}-\sqrt{3})}{6-3}=(\sqrt{6}+\sqrt{3})-(\sqrt{6}-\sqrt{3})=2\sqrt{3}\)
Bài 2 :
a, \(\dfrac{3}{\sqrt{5}-\sqrt{2}}-\dfrac{1}{\sqrt{3}+\sqrt{2}}=\dfrac{3\sqrt{5}+3\sqrt{2}}{3}-\dfrac{\sqrt{3}-\sqrt{2}}{1}\)
\(=\sqrt{5}+\sqrt{2}-\sqrt{3}+\sqrt{2}=\sqrt{5}-\sqrt{3}+2\sqrt{2}\)
b, \(\dfrac{3}{\sqrt{6}-\sqrt{3}}-\dfrac{3}{\sqrt{6}+\sqrt{3}}=\dfrac{3\sqrt{6}+3\sqrt{3}}{6-3}-\dfrac{3\sqrt{6}-3\sqrt{3}}{6-3}\)
\(=\dfrac{3\sqrt{6}+3\sqrt{3}-3\sqrt{6}+3\sqrt{3}}{3}=\dfrac{6\sqrt{3}}{3}=2\sqrt{3}\)
3)a)\(=\dfrac{\sqrt{6}\left(\sqrt{6}+1\right)}{\sqrt{6}+1}-\dfrac{\sqrt{6}\left(\sqrt{6}-1\right)}{\sqrt{6}-1}\)
\(=\sqrt{6}-\sqrt{6}=0\)
b)\(=\dfrac{\sqrt{3}\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{5}+\sqrt{2}}-\dfrac{\sqrt{2}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{5}-\sqrt{2}}\)
\(=\sqrt{3}-\sqrt{2}\)
3.
a.
\(=\frac{\sqrt{6}(\sqrt{6}+1)}{\sqrt{6}+1)}-\frac{\sqrt{6}(\sqrt{6}-1)}{\sqrt{6}-1}=\sqrt{6}-\sqrt{6}=0\)
b.
\(=\frac{\sqrt{3}(\sqrt{5}+\sqrt{2})}{\sqrt{5}+\sqrt{2}}-\frac{\sqrt{2}(\sqrt{5}-\sqrt{2})}{\sqrt{5}-\sqrt{2}}=\sqrt{3}-\sqrt{2}\)
4.
a.
\(=|\sqrt{3}+\sqrt{2}|-|\sqrt{2}-\sqrt{3}|=\sqrt{3}+\sqrt{2}-(\sqrt{3}-\sqrt{2})=2\sqrt{2}\)
b.
\(=|\sqrt{15}-4|-|3-\sqrt{15}|=(4-\sqrt{15})-(\sqrt{15}-3)=7-2\sqrt{15}\)
5.
a. ĐKXĐ: $x\geq 0$
PT $\Leftrightarrow \sqrt{6x}+\sqrt{4.6x}-6=\frac{1}{3}.\sqrt{9.6x}$
$\Leftrightarrow \sqrt{6x}+2\sqrt{6x}-6=\sqrt{6x}$
$\Leftrightarrow 3\sqrt{6x}-6=\sqrt{6x}$
$\Leftrightarrow 2\sqrt{6x}=6$
$\Leftrightarrow \sqrt{6x}=3$
$\Leftrightarrow 6x=9$
$\Leftrightarrow x=\frac{3}{2}$ (tm)
b. ĐKXĐ: $x\geq \frac{3}{2}$
PT $\Leftrightarrow \sqrt{2x-3}+\sqrt{9(2x-3)}=\sqrt{4(2x-3)}+6$
$\Leftrightarrow \sqrt{2x-3}+3\sqrt{2x-3}=2\sqrt{2x-3}+6$
$\Leftrightarrow 2\sqrt{2x-3}=6$
$\Leftrightarrow \sqrt{2x-3}=3$
$\Leftrightarrow 2x-3=9$
$\Leftrightarrow x=6$ (tm)